Soma dos termos de uma P.A. (Sn)
A soma dos n primeiros termos de uma Progressão Aritmética pode ser calculada rapidamente por duas formas equivalentes. Veja as fórmulas, um passo a passo e exercícios com soluções.
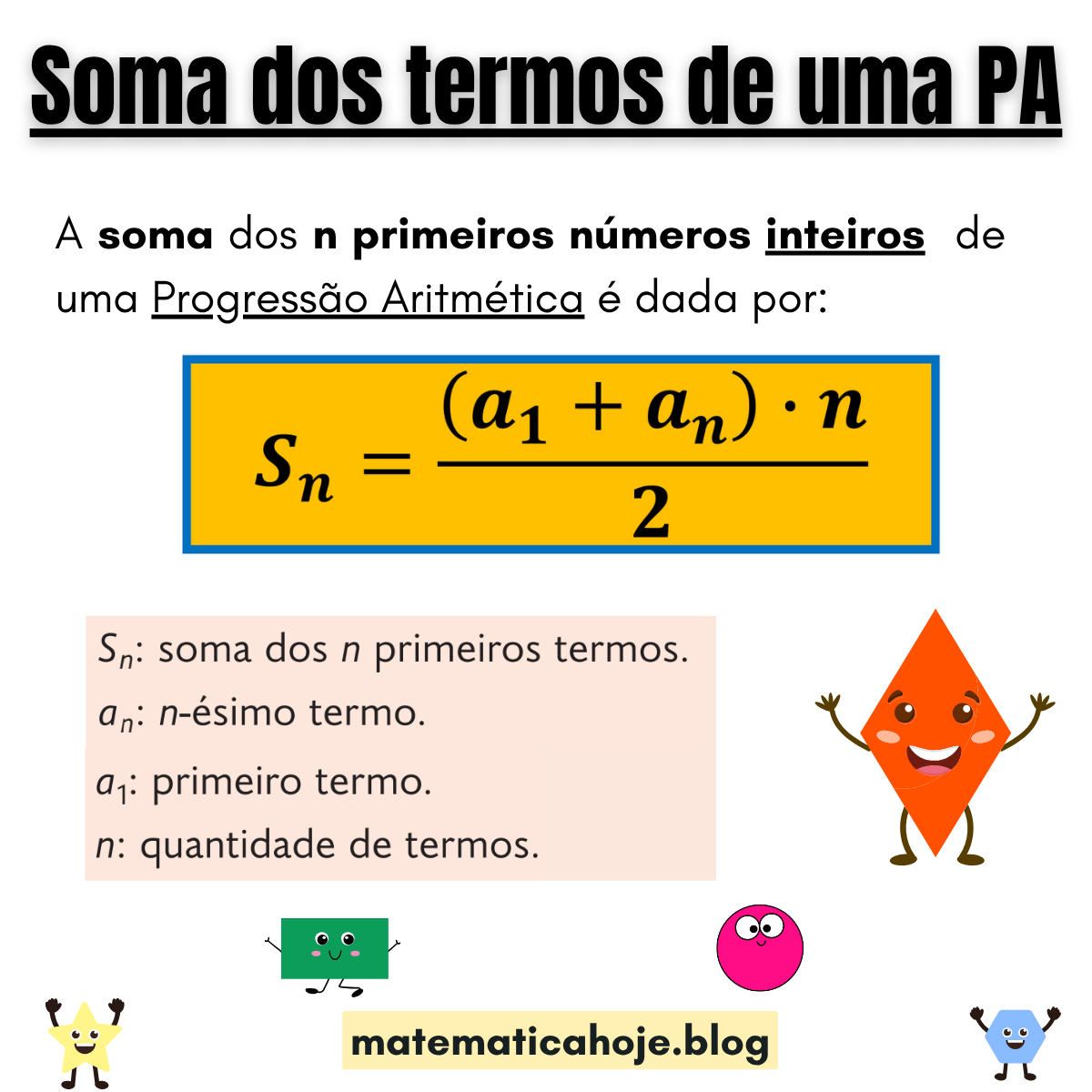
📘 Fórmulas da soma
Sn = ((a1 + an) · n) / 2
ou
Sn = n/2 · [ 2a1 + (n − 1)·r ]
- a1: primeiro termo; an: n-ésimo termo;
- r: razão da P.A.; n: quantidade de termos somados.
📗 Baixe grátis o eBook Fórmulas Matemática
Todas as fórmulas de P.A., P.G., Funções, Geometria e Estatística com quadros-resumo e exemplos. Excelente para revisão rápida.
📥 Baixar agora💡 Exemplos resolvidos (contas uma abaixo da outra)
Exemplo 1 — P.A. (3, 7, 11, …), com a₁ = 3, r = 4. Calcule S₁₀.
a₁ = 3
r = 4
n = 10
aₙ = a₁ + (n − 1)·r
a₁₀ = 3 + (10 − 1)·4
a₁₀ = 3 + 36
a₁₀ = 39
Sₙ = ((a₁ + aₙ)·n)/2
S₁₀ = ((3 + 39)·10)/2
S₁₀ = (42·10)/2
S₁₀ = 420/2
S₁₀ = 210
Exemplo 2 — Numa P.A. com a₁ = 5 e r = 3, calcule S₂₀.
n = 20
Sₙ = n/2 · [ 2a₁ + (n − 1)·r ]
S₂₀ = 20/2 · [ 2·5 + (20 − 1)·3 ]
S₂₀ = 10 · [ 10 + 19·3 ]
S₂₀ = 10 · [ 10 + 57 ]
S₂₀ = 10 · 67
S₂₀ = 670
🧠 Mapas Mentais de Matemática: revise P.A. (definição, termo geral, classificação e soma) em quadros visuais.
🔗 Artigos relacionados
🧩 Lista de Exercícios — Soma em P.A.
Metade em múltipla escolha e metade discursiva. Clique em ver solução para abrir o passo a passo.
1) (Múltipla escolha) Na P.A. com a₁ = 2, r = 3, o valor de S₁₅ é:
👀 Ver solução
a₁₅ = a₁ + (15−1)·r = 2 + 14·3 = 44
S₁₅ = ((a₁ + a₁₅)·15)/2
S₁₅ = ((2 + 44)·15)/2 = (46·15)/2 = 690/2 = 360
2) (Múltipla escolha) Em uma P.A., a₁ = 10, a₂₀ = 67. Então S₂₀ vale:
👀 Ver solução
S₂₀ = ((a₁ + a₂₀)·20)/2
S₂₀ = ((10 + 67)·20)/2 = (77·20)/2 = 1540/2 = 770
3) (Múltipla escolha) A soma dos 100 primeiros números naturais (1 a 100) é:
👀 Ver solução
P.A.: 1,2,3,...,100 ⇒ a₁=1, a₁₀₀=100, n=100
S₁₀₀ = ((1 + 100)·100)/2 = 101·50 = 5050
4) (Discursiva) Numa P.A. com a₁ = 8 e r = 5, calcule S₁₂.
👀 Ver solução
S₁₂ = n/2 · [ 2a₁ + (n−1)·r ]
S₁₂ = 12/2 · [ 2·8 + (12−1)·5 ]
S₁₂ = 6 · [ 16 + 55 ]
S₁₂ = 6 · 71
S₁₂ = 426
5) (Discursiva) Em uma P.A., a₄ = 20 e a₁₆ = 68. Encontre S₁₆.
👀 Ver solução
r = (a₁₆ − a₄)/(16 − 4) = (68 − 20)/12 = 48/12 = 4
a₁ = a₄ − 3r = 20 − 12 = 8
a₁₆ = 68 (dado)
S₁₆ = ((a₁ + a₁₆)·16)/2
S₁₆ = ((8 + 68)·16)/2 = (76·16)/2 = 1216/2 = 608
6) (Discursiva) A soma dos n primeiros termos de uma P.A. é Sₙ = 3n² + n. Determine a₁ e a razão r.
👀 Ver solução
Em P.A.: aₙ = Sₙ − Sₙ₋₁
Sₙ = 3n² + n
Sₙ₋₁ = 3(n−1)² + (n−1) = 3(n² − 2n + 1) + n − 1 = 3n² − 6n + 3 + n − 1
Sₙ₋₁ = 3n² − 5n + 2
aₙ = (3n² + n) − (3n² − 5n + 2) = 6n − 2
Logo, a₁ = 6·1 − 2 = 4 e r = a₂ − a₁ = (6·2−2) − 4 = (12−2) − 4 = 6

























