Hoje vamos aprender o Teorema da Bissetriz Externa, um resultado muito importante em geometria, especialmente quando lidamos com triângulos e divisão proporcional de segmentos. Ele complementa o Teorema da Bissetriz Interna, mas tem uma diferença crucial: a bissetriz agora não divide o ângulo dentro do triângulo, mas sim o prolongamento de um dos lados.
Essa configuração aparece com frequência em questões do ENEM, Olimpíadas e concursos matemáticos, por isso é importante dominar a ideia e saber aplicar a fórmula corretamente.
1️⃣ O que é a bissetriz externa?
Quando prolongamos um dos lados do triângulo, criamos um ângulo externo. A bissetriz externa é o segmento que divide esse ângulo externo em duas partes iguais.
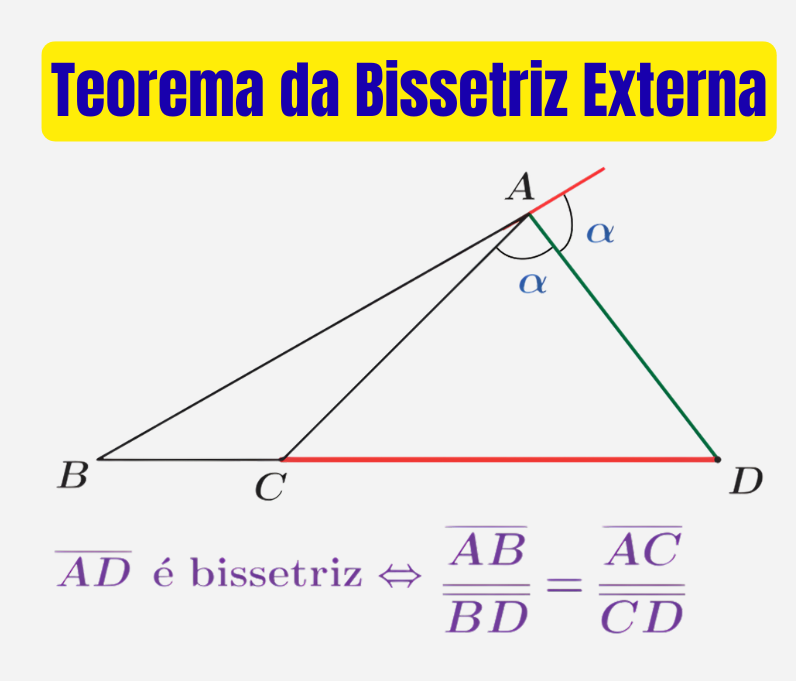
Na imagem, o segmento $\\overline{AD}$ divide o ângulo externo do triângulo em duas partes iguais, representadas por $\alpha$:
$\angle BAD = \angle DAC = \\alpha$.
2️⃣ O Enunciado do Teorema
Se no triângulo $ABC$ prolongamos o lado $BC$ até $D$, e o segmento $\\overline{AD}$ é bissetriz do ângulo externo em $A$, então:
\[ \frac{AB}{AC} = \frac{BD}{DC} \]
Mas atenção: agora estamos trabalhando com um lado prolongado, portanto a fórmula equivalente usada na literatura é:
\[ \overline{AD}\ \text{é bissetriz externa} \Rightarrow \frac{\overline{AB}}{\overline{BD}} = \frac{\overline{AC}}{\overline{CD}}. \]
Perceba que a estrutura da fórmula é parecida com a da bissetriz interna — porém agora os segmentos correspondentes estão no prolongamento do lado.
3️⃣ Diferença entre bissetriz interna e externa
| Bissetriz Interna | Bissetriz Externa |
|---|---|
| Divide o ângulo dentro do triângulo | Divide o ângulo externo (lado prolongado) |
| $\displaystyle \frac{AB}{AC} = \frac{BD}{DC}$ | $\displaystyle \frac{AB}{AC} = \frac{BD}{DC}$ (para prolongamento) |
Apesar das fórmulas parecerem iguais, a interpretação geométrica é diferente.
4️⃣ Exemplo Resolvido — Encontrando Segmento
No triângulo $ABC$, o lado $BC$ foi prolongado até $D$. A bissetriz externa $AD$ divide o ângulo externo em duas partes iguais. Se:
- $AB = 9\,\text{cm}$
- $AC = 6\,\text{cm}$
- $BD = 14\,\text{cm}$
Calcule o valor de $DC$.
\[ \frac{AB}{AC} = \frac{BD}{DC} \Rightarrow \frac{9}{6} = \frac{14}{DC} \]
\[ \begin{aligned} \frac{9}{6} &= \frac{14}{DC} \\ \frac{3}{2} &= \frac{14}{DC} \\ 3 \cdot DC &= 2 \cdot 14 \\ 3\,DC &= 28 \\ DC &= \frac{28}{3} \\ DC &\approx 9{,}33\,\text{cm} \end{aligned} \]
Resposta: $DC \approx 9{,}33\,\text{cm}$
5️⃣ Exemplo Aplicado ao ENEM
Em um triângulo, o lado $BC$ é prolongado até $D$. Sabe-se que $AD$ é bissetriz externa e:
- $BD = 10\,\text{cm}$
- $DC = 5\,\text{cm}$
- $AC = 12\,\text{cm}$
Determine o valor de $AB$.
\[ \frac{AB}{AC} = \frac{BD}{DC} \Rightarrow \frac{AB}{12} = \frac{10}{5} \Rightarrow \frac{AB}{12} = 2 \]
\[ \begin{aligned} AB &= 2 \cdot 12 \\ AB &= 24\,\text{cm} \end{aligned} \]
Resposta: $AB = 24\,\text{cm}$
6️⃣ Quando usar o Teorema?
Use o Teorema da Bissetriz Externa quando:
- Existe um triângulo;
- Um lado foi prolongado;
- O segmento divide o ângulo externo ao meio.
Se essas três condições estiverem presentes, a fórmula pode ser aplicada.
🎯 Resumo Final
\[ \boxed{\frac{AB}{AC} = \frac{BD}{DC}} \]
A bissetriz externa cria uma divisão proporcional semelhante à da bissetriz interna, mas agora envolvendo o prolongamento de um dos lados do triângulo. Esse teorema é indispensável para resolver problemas de geometria envolvendo ângulos externos.













