Teorema de Pitágoras: conceito, fórmulas, exemplos e exercícios
O Teorema de Pitágoras relaciona os lados de um triângulo retângulo e é base para questões de geometria, trigonometria, ENEM, OBMEP e concursos. Neste guia, você aprende a usar a fórmula, visualiza a ideia por áreas, resolve exemplos e pratica com exercícios.
O que é o Teorema de Pitágoras
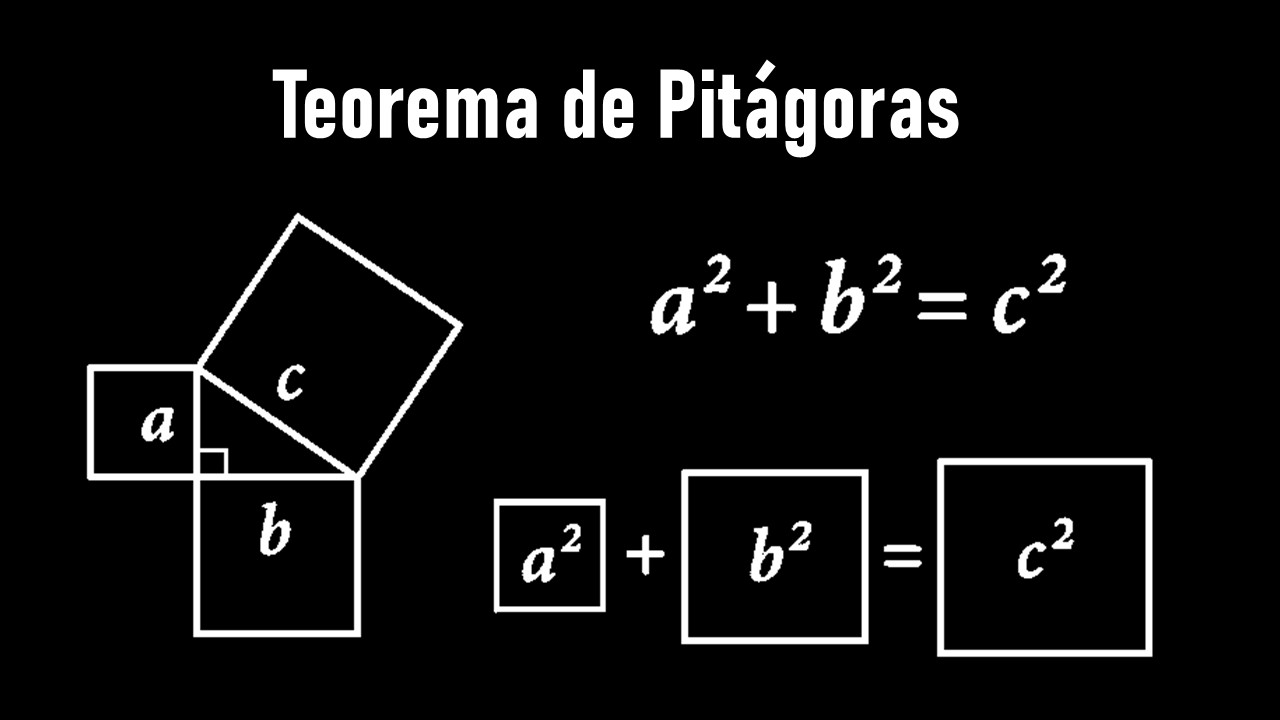
Em todo triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos:
\( c^2 = a^2 + b^2 \)
Onde c é a hipotenusa (o maior lado, oposto ao ângulo de 90°) e a, b são os catetos.
Fórmulas mais usadas
Hipotenusa: \( c = \sqrt{a^2+b^2} \)
Cateto a: \( a = \sqrt{c^2-b^2} \)
Cateto b: \( b = \sqrt{c^2-a^2} \)
Visualização por áreas
Se os quadrados sobre os catetos têm áreas \(a^2\) e \(b^2\), e o quadrado sobre a hipotenusa tem área \(c^2\), então:
\( a^2 + b^2 = c^2 \)
Essa visão explica por que a relação funciona independentemente das medidas: ela compara áreas geométricas, não apenas números.
Exemplos resolvidos (abre/fecha)
Exemplo 1 Calcular a hipotenusa para catetos 3 cm e 4 cm
\( c^2=3^2+4^2=9+16=25 \Rightarrow c=5\text{ cm} \).
Exemplo 2 Descobrir o cateto faltante: \(c=13\) m e \(a=5\) m
\( b=\sqrt{13^2-5^2}=\sqrt{169-25}=\sqrt{144}=12\text{ m} \).
Exemplo 3 Diagonal de um retângulo 6 m × 8 m
\( d=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10\text{ m} \).
Exercícios para praticar
1) Altura da escada
Uma escada de 15 m está apoiada em uma parede. A base está a 9 m da parede. Qual a altura atingida?
Ver solução
\(h=\sqrt{15^2-9^2}=\sqrt{225-81}=\sqrt{144}=12\text{ m}\).
2) Distância entre pontos
Um ponto A está 5 m ao leste e 12 m ao norte de B. Qual a distância direta AB?
Ver solução
\( AB=\sqrt{5^2+12^2}=\sqrt{25+144}=\sqrt{169}=13\text{ m}\).
3) Quadrado e diagonal
O lado de um quadrado mede 7 cm. Qual a diagonal?
Ver solução
\( d=\sqrt{7^2+7^2}=\sqrt{98}=7\sqrt{2}\text{ cm}\).
Leituras relacionadas no Matemática Hoje
Continue estudando com nossos materiais premium
Lista de Exercícios — Teorema de Pitágoras (Múltipla Escolha)
Resolva os exercícios abaixo e teste seus conhecimentos sobre o Teorema de Pitágoras. As alternativas corretas estão disponíveis no sistema de abre/fecha.
1) Hipotenusa simples
Um triângulo retângulo possui catetos medindo \(6\) cm e \(8\) cm. Qual é a medida da hipotenusa?
- A) 8 cm
- B) 9 cm
- C) 10 cm
- D) 11 cm
- E) 12 cm
Ver solução
\(c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10\ \text{cm}\). Alternativa correta: C
2) Cateto desconhecido
Em um triângulo retângulo, a hipotenusa mede \(17\) cm e um dos catetos mede \(8\) cm. Calcule o outro cateto.
- A) 12 cm
- B) 13 cm
- C) 14 cm
- D) 15 cm
- E) 16 cm
Ver solução
\(b = \sqrt{17^2 – 8^2} = \sqrt{289 – 64} = \sqrt{225} = 15\ \text{cm}\). Alternativa correta: D
3) Distância entre dois pontos
Um barco parte de um ponto \(A\) e navega \(9\) km para o norte e \(12\) km para o leste. Qual a distância direta entre o ponto inicial e o final?
- A) 12 km
- B) 14 km
- C) 15 km
- D) 16 km
- E) 18 km
Ver solução
\(d = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15\ \text{km}\). Alternativa correta: C
4) Diagonal de um quadrado
Um quadrado tem lado medindo \(5\) cm. Qual é a medida da diagonal?
- A) \(5\sqrt{2}\) cm
- B) \(6\sqrt{2}\) cm
- C) \(7\sqrt{2}\) cm
- D) \(8\sqrt{2}\) cm
- E) \(9\sqrt{2}\) cm
Ver solução
\(d = \sqrt{5^2 + 5^2} = \sqrt{25 + 25} = \sqrt{50} = 5\sqrt{2}\ \text{cm}\). Alternativa correta: A
5) Diagonal de um retângulo
Um retângulo tem dimensões \(9\) cm por \(12\) cm. Determine a medida da diagonal.
- A) 13 cm
- B) 14 cm
- C) 15 cm
- D) 16 cm
- E) 17 cm
Ver solução
\(d = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15\ \text{cm}\). Alternativa correta: C
6) Escada apoiada
Uma escada de \(7\) m está apoiada em uma parede, formando um ângulo reto com o chão. A base da escada está a \(4\) m da parede. Qual a altura que a escada alcança?
- A) 4,2 m
- B) 5,3 m
- C) 5,7 m
- D) 6,1 m
- E) 6,5 m
Ver solução
\(h = \sqrt{7^2 – 4^2} = \sqrt{49 – 16} = \sqrt{33} \approx 5,74\ \text{m}\). Alternativa correta: C
7) Altura de triângulo equilátero
Um triângulo equilátero tem lado de \(10\) cm. Qual é a medida da altura?
- A) \(5\sqrt{2}\) cm
- B) \(5\sqrt{3}\) cm
- C) \(6\sqrt{3}\) cm
- D) \(7\sqrt{2}\) cm
- E) \(8\sqrt{2}\) cm
Ver solução
\(h = \sqrt{10^2 – 5^2} = \sqrt{100 – 25} = \sqrt{75} = 5\sqrt{3}\ \text{cm}\). Alternativa correta: B
8) Área de triângulo retângulo
Um triângulo retângulo possui hipotenusa de \(25\) cm e um cateto de \(7\) cm. Qual é a área do triângulo?
- A) 72 cm²
- B) 78 cm²
- C) 80 cm²
- D) 84 cm²
- E) 90 cm²
Ver solução
\(b = \sqrt{25^2 – 7^2} = \sqrt{625 – 49} = \sqrt{576} = 24\ \text{cm}\) \(A = \frac{7 \cdot 24}{2} = 84\ \text{cm}^2\). Alternativa correta: D
9) Distância espacial
Um ponto \(P\) possui coordenadas \((3, 4, 12)\) e o ponto \(Q\) está na origem. Qual é a distância entre os dois pontos?
- A) 10
- B) 11
- C) 12
- D) 13
- E) 14
Ver solução
\(d = \sqrt{3^2 + 4^2 + 12^2} = \sqrt{9 + 16 + 144} = \sqrt{169} = 13\). Alternativa correta: D
10) Aplicação avançada — fio no terreno
Um terreno retangular mede \(30\) m de largura e \(40\) m de comprimento. Um fio será estendido da base até o vértice oposto. Qual será o comprimento do fio?
- A) 45 m
- B) 48 m
- C) 50 m
- D) 52 m
- E) 55 m
Ver solução
\(d = \sqrt{30^2 + 40^2} = \sqrt{900 + 1600} = \sqrt{2500} = 50\ \text{m}\). Alternativa correta: C

























