Teorema de Stewart: Demonstração, Exemplos e Aplicações
O Teorema de Stewart é um dos resultados mais elegantes da geometria dos triângulos. Ele relaciona os comprimentos dos lados de um triângulo com uma ceviana qualquer, permitindo cálculos que envolvem medianas, bissetrizes e outros segmentos notáveis. Seu estudo é fundamental para compreender propriedades mais avançadas da geometria e também aparece com frequência em provas de vestibulares e olimpíadas matemáticas.
O que diz o Teorema de Stewart?
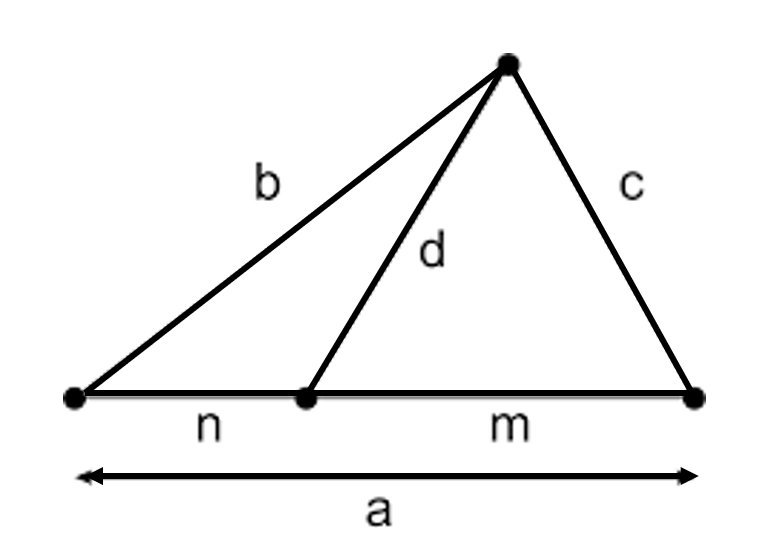
Considere um triângulo \(ABC\), em que:
- \( a = BC \)
- \( b = AC \)
- \( c = AB \)
- O ponto \( D \) está sobre o lado \( BC \), de forma que \( BD = m \) e \( DC = n \)
- A ceviana \( AD = d \)
\[ b^{2} \cdot m + c^{2} \cdot n = a \cdot \left(d^{2} + mn\right) \]
Essa relação mostra como o comprimento da ceviana \( d \) pode ser expresso em termos dos lados do triângulo e das subdivisões \( m \) e \( n \). Trata-se de um teorema que generaliza vários outros resultados clássicos, como o Teorema de Apolônio.
Relação com outros pontos notáveis
O Teorema de Stewart se conecta de forma direta aos pontos notáveis do triângulo, pois ao escolher o ponto \( D \) em posições específicas, obtemos resultados famosos:
- Mediana e Baricentro: quando \( D \) é o ponto médio de \( BC \), temos o Teorema de Apolônio.
- Bissetriz e Incentro: quando \( AD \) é a bissetriz interna, o teorema ajuda a calcular o comprimento da ceviana.
- Altura e Ortocentro: quando \( AD \) é a altura, o Teorema de Stewart pode ser adaptado.
- Mediatriz e Circuncentro: embora não seja ceviana, a mediatriz se conecta ao estudo das relações métricas.
Casos particulares
Teorema de Apolônio
Se o ponto \( D \) for o ponto médio de \( BC \), temos \( m = n = \tfrac{a}{2} \). Substituindo na fórmula:
Esse é exatamente o Teorema de Apolônio, que mostra a relação entre lados e medianas de um triângulo.
Demonstração resumida
A demonstração do Teorema de Stewart pode ser feita a partir da lei dos cossenos aplicada nos triângulos \( ABD \) e \( ADC \). Aplicando a lei dos cossenos em cada um e somando os resultados, chegamos à identidade apresentada. Esse processo ilustra como a trigonometria pode fundamentar relações geométricas.
Exemplo resolvido
Exemplo: Num triângulo \(ABC\), temos \(AB = 10\), \(AC = 8\), \(BC = 12\). O ponto \(D\) divide \(BC\) em \(BD = 5\) e \(DC = 7\). Calcule \(AD\).
Solução:
Aplicando o Teorema de Stewart:
\[ b^{2}m + c^{2}n = a(d^{2} + mn) \] \[ 8^{2} \cdot 5 + 10^{2} \cdot 7 = 12 \cdot (d^{2} + 35) \] \[ 320 + 700 = 12d^{2} + 420 \] \[ 1020 = 12d^{2} + 420 \] \[ 600 = 12d^{2} \] \[ d^{2} = 50 \] \[ d = \sqrt{50} = 5\sqrt{2} \]Importância do Teorema de Stewart
O Teorema de Stewart é um recurso poderoso na resolução de problemas que envolvem cevianas em triângulos. Ele aparece como ferramenta de apoio em questões que pedem cálculo de medianas, bissetrizes e alturas, além de ser um passo intermediário em demonstrações mais complexas.
Estudar este teorema reforça o entendimento sobre propriedades dos triângulos, incluindo suas classificações quanto aos lados e quanto aos ângulos, além de aprofundar o domínio sobre as propriedades dos ângulos externos.
Conclusão
O Teorema de Stewart é uma ferramenta versátil da geometria, permitindo a resolução de problemas que envolvem qualquer ceviana. Ele conecta conceitos fundamentais e gerais da geometria com casos particulares famosos, como o Teorema de Apolônio. Ao dominar esse teorema, o estudante amplia suas habilidades para resolver questões desafiadoras em provas e concursos.

























