Teorema de Tales
O Teorema de Tales é um dos pilares da geometria, relacionando proporções entre segmentos de retas paralelas cortadas por duas transversais.
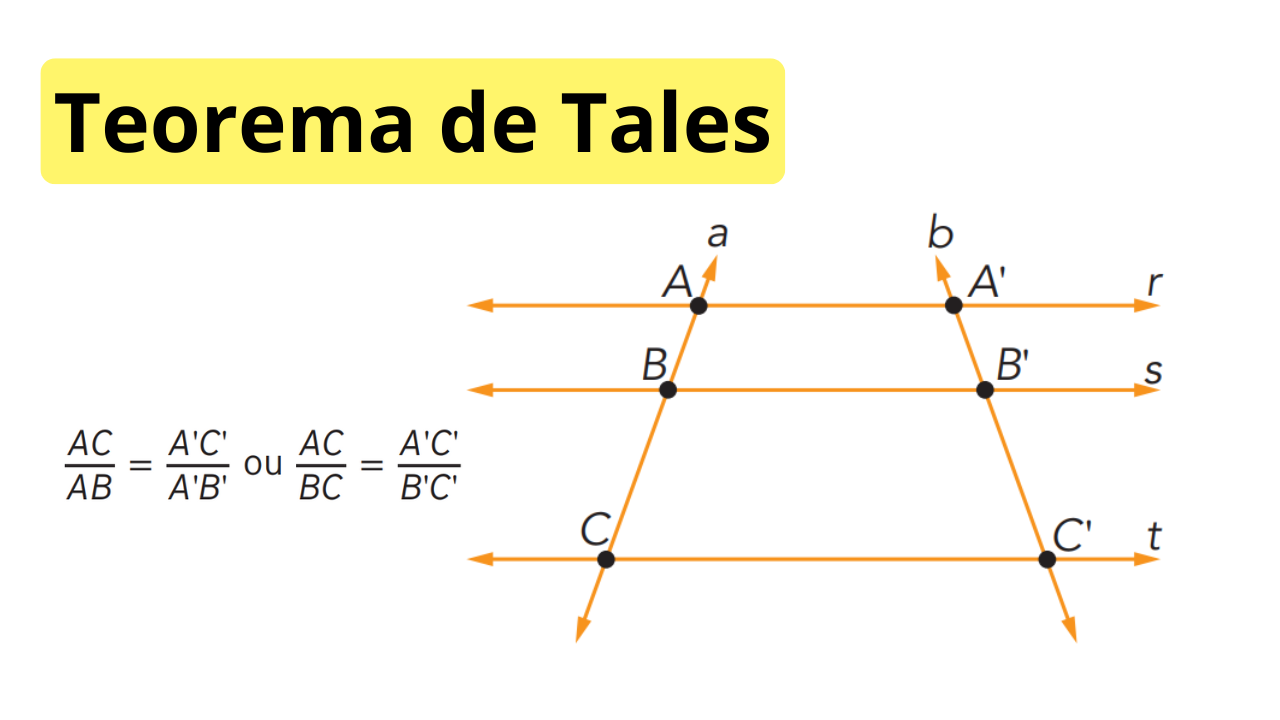
1) Enunciado do Teorema de Tales
Se duas retas distintas são cortadas por retas paralelas, então os segmentos determinados nessas retas são proporcionais.
2) Interpretação geométrica
No diagrama, as retas \(r\), \(s\) e \(t\) são paralelas. Elas são cortadas pelas retas \(a\) e \(b\), que se encontram nos pontos \(A, B, C\) e \(A’, B’, C’\). Os segmentos formados obedecem a uma relação de proporcionalidade.
3) Consequências do Teorema
- Base para a definição de triângulos semelhantes;
- Utilizado em problemas de proporcionalidade e escalas;
- Fundamental em aplicações práticas, como medições indiretas em engenharia e arquitetura.
4) Exemplos resolvidos
Exemplo 1: Na figura, considere \(AB=4\), \(BC=6\) e \(A’B’=8\). Determine \(B’C’\).
Mostrar solução
Pelo Teorema de Tales: \(\dfrac{AC}{BC}=\dfrac{A’C’}{B’C’}\). Como \(AC=AB+BC=10\), temos:
\(\dfrac{10}{6}=\dfrac{A’C’}{B’C’}\). Mas \(A’C’=A’B’+B’C’=8+B’C’\). Assim:
\(\dfrac{10}{6}=\dfrac{8+B’C’}{B’C’}\Rightarrow 10B’C’=6(8+B’C’)\Rightarrow 10B’C’=48+6B’C’\Rightarrow 4B’C’=48\Rightarrow B’C’=12.\)
Exemplo 2: Uma sombra de um poste de 5 m mede 4 m. Um homem projeta sombra de 1,6 m. Qual a altura do homem?
Mostrar solução
Pelo Teorema de Tales: \(\dfrac{altura\ do\ poste}{sombra\ do\ poste}=\dfrac{altura\ do\ homem}{sombra\ do\ homem}\).
\(\dfrac{5}{4}=\dfrac{h}{1,6}\Rightarrow h=\dfrac{5\cdot1,6}{4}=2\;\text{m}\).
📘Exercícios – Múltipla Escolha (com solução)
Marque a alternativa correta. Use o Teorema de Tales e proporções.
1) Em retas paralelas, \(AB=3\), \(BC=9\) e \(A’B’=4\). Calcule \(B’C’\).
- 6
- 8
- 10
- 12
Ver solução
\(AC=3+9=12\). Pelo Teorema de Tales: \(\dfrac{AC}{BC}=\dfrac{A’C’}{B’C’}\Rightarrow\dfrac{12}{9}=\dfrac{4+B’C’}{B’C’}\).
\(12B’C’=36+9B’C’\Rightarrow 3B’C’=36\Rightarrow B’C’=12\).
2) Um prédio de 20 m projeta sombra de 12 m. Um poste projeta sombra de 3 m. A altura do poste é:
- 4 m
- 5 m
- 6 m
- 7 m
Ver solução
\(\dfrac{20}{12}=\dfrac{h}{3}\Rightarrow h=\dfrac{20}{12}\cdot3=5\text{ m}\).
3) Em uma maquete, 2 cm representam 5 m. Quantos cm representam 25 m?
- 5 cm
- 8 cm
- 10 cm
- 12 cm
Ver solução
Escala proporcional: \(x=2\cdot\dfrac{25}{5}=10\text{ cm}\).
4) Um triângulo é cortado por uma paralela à base. Em uma lateral os segmentos são 6 cm e 9 cm. O segmento correspondente ao de 6 cm na outra lateral mede 8 cm. O outro segmento mede:
- 10 cm
- 12 cm
- 14 cm
- 16 cm
Ver solução
\(\dfrac{6}{9}=\dfrac{8}{x}\Rightarrow x=\dfrac{9\cdot8}{6}=12\text{ cm}\).
5) Uma escada de 4 m projeta sombra de 2,5 m. No mesmo instante, um poste projeta sombra de 5 m. A altura do poste é:
- 6 m
- 7 m
- 8 m
- 10 m
Ver solução
\(\dfrac{4}{2{,}5}=\dfrac{h}{5}\Rightarrow h=5\cdot\dfrac{4}{2{,}5}=8\text{ m}\).
6) Sabendo que \(AB:BC=2:5\) e \(B’C’=15\) cm, encontre \(A’C’\).
- 18 cm
- 21 cm
- 24 cm
- 25 cm
Ver solução
\(AC/BC=(2+5)/5=7/5\). Logo \(A’C’=(7/5)\cdot B’C’=(7/5)\cdot15=21\text{ cm}\).
7) Em retas paralelas, \(AB=4\), \(A’B’=6\) e \(B’C’=9\). Calcule \(BC\).
- 4
- 5
- 6
- 7
Ver solução
\(A’C’=6+9=15\). \(\dfrac{AC}{AB}=\dfrac{A’C’}{A’B’}=\dfrac{15}{6}=2{,}5\Rightarrow AC=2{,}5\cdot4=10\).
\(BC=AC-AB=10-4=6\).
8) Um bastão de 1,2 m projeta sombra de 0,8 m. Uma árvore projeta sombra de 6 m. A altura da árvore é:
- 7,5 m
- 8 m
- 9 m
- 9,6 m
Ver solução
\(\dfrac{1{,}2}{0{,}8}=\dfrac{H}{6}\Rightarrow H=6\cdot1{,}5=9\text{ m}\).
Dica: sempre some os dois segmentos de uma transversal para obter o comprimento total \(AC\) (ou \(A’C’\)) quando necessário.
6) Links para aprofundar
O Teorema de Tales conecta medições diretas e indiretas, tornando possível resolver problemas do dia a dia com raciocínio geométrico.