Teorema de Tales, Corolário, Corolário Inverso e Teorema da Bissetriz Interna em um único lugar: enunciados, fórmulas, interpretações, exemplos e exercícios.
Os Teoremas de Tales formam um bloco fundamental da Geometria Plana. Eles aparecem com muita frequência no ENEM, em vestibulares, na OBMEP e em concursos públicos. Dominar esse grupo de resultados permite resolver uma grande variedade de questões envolvendo triângulos, paralelismo, escalas e semelhança de figuras.
Mapa visual dos Teoremas de Tales
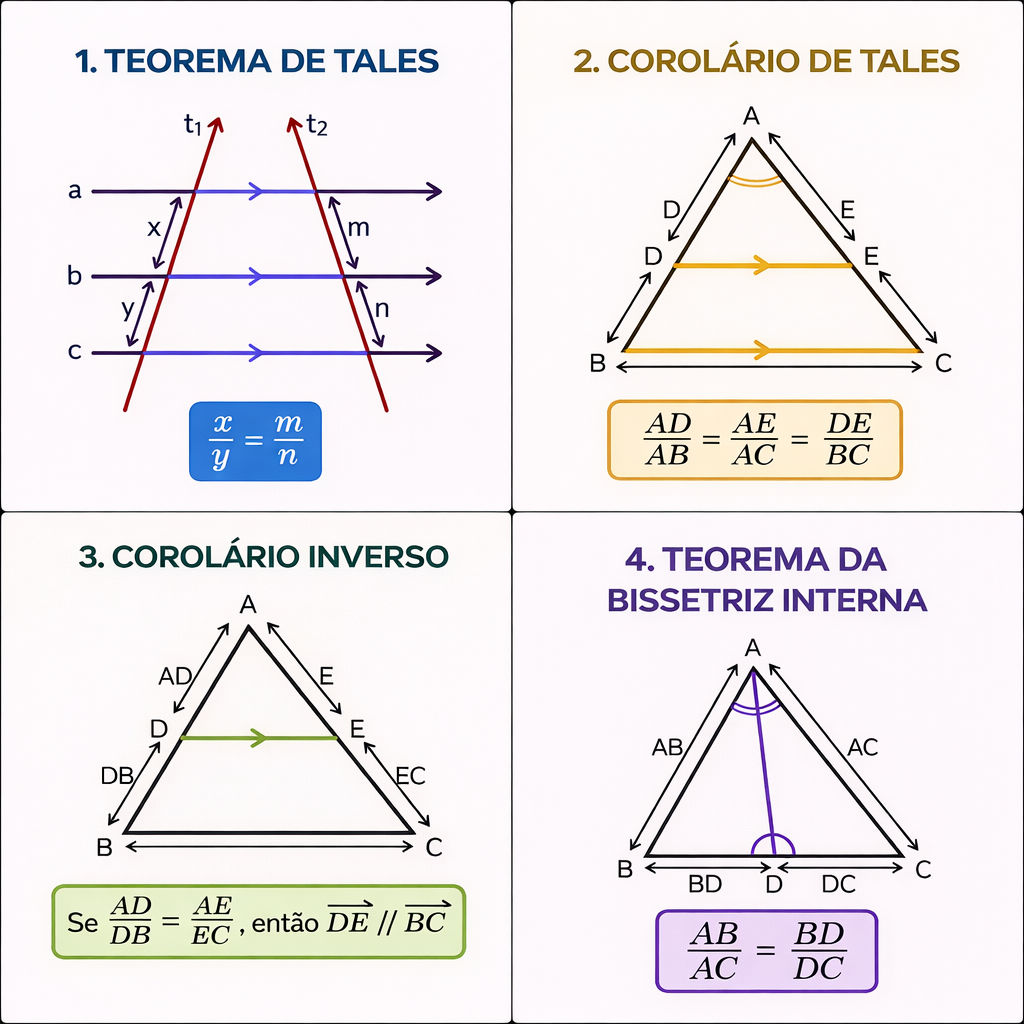
Na imagem, temos um painel com quatro blocos principais:
- 1. Teorema de Tales (paralelas e transversais);
- 2. Corolário de Tales (triângulo cortado por segmento paralelo);
- 3. Corolário Inverso (proporções garantem paralelismo);
- 4. Teorema da Bissetriz Interna (bissetriz divide o lado oposto proporcionalmente).
1. Teorema de Tales
O Teorema de Tales relaciona segmentos formados quando duas ou mais retas paralelas são cortadas por retas transversais. Ele garante que os segmentos correspondentes nessas transversais são proporcionais.
No painel, as paralelas são as retas \(a\), \(b\) e \(c\). As transversais são \(t_1\) e \(t_2\), formando os segmentos \(x\) e \(y\) numa transversal, e \(m\) e \(n\) na outra. Assim:
\(\displaystyle \frac{x}{y} = \frac{m}{n}\)
Exemplo 1 — Cálculo de segmento em transversais
Suponha que em duas transversais cortadas por três paralelas temos a relação:
\(\displaystyle \frac{x}{5} = \frac{6}{9}\)
Para encontrar \(x\), fazemos:
- Produto em cruz: \(9x = 5 \cdot 6\);
- \(9x = 30\);
- \(x = \dfrac{30}{9} = \dfrac{10}{3} \approx 3{,}33\).
Resposta: \(x = \dfrac{10}{3}\).
Exemplo 2 — Escala em mapas
Num mapa, um trecho de estrada mede 4 cm e corresponde a 24 km na realidade. Outro trecho mede 6 cm. Qual o comprimento real desse segundo trecho?
Usamos a proporção entre “medida no mapa” e “medida real”:
\(\displaystyle \frac{4}{24} = \frac{6}{x}\)
Produto em cruz:
\(4x = 24 \cdot 6 \Rightarrow 4x = 144 \Rightarrow x = 36\)
Resposta: o trecho real mede 36 km.
Para uma explicação ainda mais detalhada e focada nesse teorema, veja o artigo específico: Teorema de Tales — o que é, fórmula e exemplos.
2. Corolário do Teorema de Tales
O Corolário do Teorema de Tales é uma aplicação direta de Tales dentro de um triângulo. Quando traçamos um segmento paralelo a um lado do triângulo, os outros dois lados são divididos de forma proporcional.
\(\displaystyle \frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC}\)
\(\displaystyle \frac{AD}{DB} = \frac{AE}{EC}\)
Isso acontece porque o triângulo \(ADE\) é semelhante ao triângulo \(ABC\). As razões entre lados correspondentes são iguais, o que produz todas as proporções mostradas na imagem.
Exemplo 3 — Encontrando um lado do triângulo
No triângulo \(ABC\), \(DE\parallel BC\). Sabemos que \(AD = 3\), \(AB = 9\) e \(AE = 4\). Determine o valor de \(AC\).
Pela proporcionalidade:
\(\displaystyle \frac{AD}{AB} = \frac{AE}{AC}\)
Substituindo:
\(\displaystyle \frac{3}{9} = \frac{4}{AC}\)
Simplificando \(\dfrac{3}{9} = \dfrac{1}{3}\):
\(\displaystyle \frac{1}{3} = \frac{4}{AC}\)
Produto em cruz: \(1 \cdot AC = 3 \cdot 4 \Rightarrow AC = 12\).
Resposta: \(AC = 12\).
Aprofunde esse resultado em: Corolário do Teorema de Tales — explicação e exemplos.
3. Corolário Inverso de Tales
O Corolário Inverso de Tales funciona como um critério de paralelismo. Em vez de partirmos de um segmento paralelo para concluir a proporcionalidade, fazemos o contrário: se as razões entre os segmentos forem iguais, então o segmento traçado será paralelo a um lado do triângulo.
\(\displaystyle \frac{AD}{DB} = \frac{AE}{EC}\),
então o segmento \(DE\) é paralelo ao lado \(BC\), isto é, \(DE \parallel BC\).Geometricamente, isso garante que o triângulo \(ADE\) é semelhante ao triângulo \(ABC\). E, para que essa semelhança ocorra, o segmento \(DE\) precisa “imitar” o lado \(BC\), sendo paralelo a ele.
Exemplo 4 — Verificando se o segmento é paralelo
No triângulo \(ABC\), \(D\in AB\) e \(E\in AC\). Sabemos que:
- \(AD = 4\), \(DB = 8\);
- \(AE = 3\), \(EC = 6\).
Verifique se \(DE\) é paralelo a \(BC\).
Calculamos as razões:
\(\displaystyle \frac{AD}{DB} = \frac{4}{8} = \frac{1}{2}\)
\(\displaystyle \frac{AE}{EC} = \frac{3}{6} = \frac{1}{2}\)
Como as razões são iguais, temos:
\(\displaystyle \frac{AD}{DB} = \frac{AE}{EC}\)
Logo, pelo Corolário Inverso de Tales, \(DE\parallel BC\).
Veja o desenvolvimento completo desse teorema em: Corolário Inverso de Tales — critério de paralelismo.
4. Teorema da Bissetriz Interna
O Teorema da Bissetriz Interna trata de um caso especial: quando a reta considerada é a bissetriz interna de um ângulo do triângulo. Esse teorema mostra como ela divide o lado oposto de forma proporcional aos demais lados do triângulo.
\(\displaystyle \frac{AB}{AC} = \frac{BD}{DC}\)
Ou seja, a bissetriz interna divide o lado oposto em segmentos proporcionais aos lados que formam o ângulo.Exemplo 5 — Aplicando a bissetriz interna
No triângulo \(ABC\), o segmento \(AD\) é bissetriz interna do ângulo em \(A\). Sabemos que \(AB = 8\) cm, \(AC = 12\) cm e \(BD = 5\) cm. Calcule \(DC\).
Utilizamos a relação:
\(\displaystyle \frac{AB}{AC} = \frac{BD}{DC}\)
Substituindo:
\(\displaystyle \frac{8}{12} = \frac{5}{DC}\)
Simplificando a fração: \(\dfrac{8}{12} = \dfrac{2}{3}\).
\(\displaystyle \frac{2}{3} = \frac{5}{DC}\)
Produto em cruz:
\(2\cdot DC = 3\cdot 5 \Rightarrow 2\,DC = 15\)
Logo:
\(DC = \dfrac{15}{2} = 7{,}5 \text{ cm}\).
Resposta: \(DC = 7{,}5\) cm.
Para ver mais aplicações e exercícios, acesse: Teorema da Bissetriz Interna — teoria e exercícios resolvidos.
Lista de exercícios gerais sobre os Teoremas de Tales
Use esta lista para revisar de forma integrada todos os resultados estudados.
- Teorema de Tales: Três paralelas cortam duas transversais. Na primeira transversal, os segmentos medem 3 cm e 7 cm. Na segunda, o menor segmento mede 6 cm. Determine o outro segmento.
- Corolário de Tales: No triângulo \(ABC\), o segmento \(DE\) é paralelo a \(BC\). Se \(AD = 4\), \(AB = 10\) e \(BC = 9\), calcule o comprimento de \(DE\).
- Corolário Inverso: Em um triângulo, \(D\in AB\) e \(E\in AC\). Temos \(AD = 2\) cm, \(DB = 4\) cm, \(AE = 3\) cm e \(EC = 6\) cm. Verifique se \(DE\) é paralelo a \(BC\).
- Bissetriz Interna: No triângulo \(ABC\), a bissetriz interna do ângulo em \(A\) encontra o lado \(BC\) em \(D\). Se \(AB = 5\) cm, \(AC = 7\) cm e \(BD = 6\) cm, determine \(DC\).
- Integração: Explique, com suas palavras, como o Teorema de Tales e seus corolários ajudam a demonstrar o Teorema da Bissetriz Interna. (Dica: pense em triângulos semelhantes.)
Você pode transformar esses exercícios em questões de múltipla escolha para provas simuladas, listas de revisão ou atividades da sala de aula.
Quer dominar Geometria Plana de uma vez?
Os Teoremas de Tales são apenas uma parte da Geometria que mais cai em provas. Para estudar com organização e ganhar confiança, use os materiais do Matemática Hoje:
- Curso Matemática Básica: Do Zero à Confiança Prática
- Pacote com 10 eBooks de Matemática
- Questões Comentadas de Matemática do ENEM
Use este guia como referência e volte sempre que precisar revisar os Teoremas de Tales.
Leia também no Matemática Hoje
- Mapas Mentais de Matemática
- FGV 2025 – Matemática para Concurso
- Grupo gratuito de Matemática no WhatsApp — receba questões, resumos e novidades.