Teste da Primeira Derivada — Guia Completo
O Teste da Primeira Derivada é um método prático para determinar os intervalos de crescimento e decrescimento de uma função e identificar seus máximos e mínimos locais. Neste guia, vamos entender o conceito, aplicar a regra em exemplos e interpretar os resultados com gráficos.
1) O que é o Teste da Primeira Derivada?
Seja \(f\) uma função contínua e derivável em um intervalo \(I\). A primeira derivada \(f'(x)\) indica a inclinação da reta tangente à curva da função, permitindo identificar onde \(f\) é crescente ou decrescente.
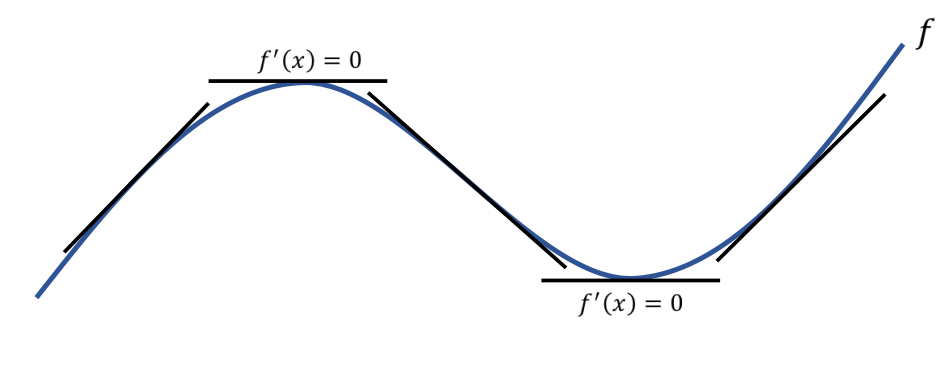
2) Teorema do Teste da Primeira Derivada
O teorema estabelece que, em regiões onde a derivada muda de sinal, identificamos máximos e mínimos locais:
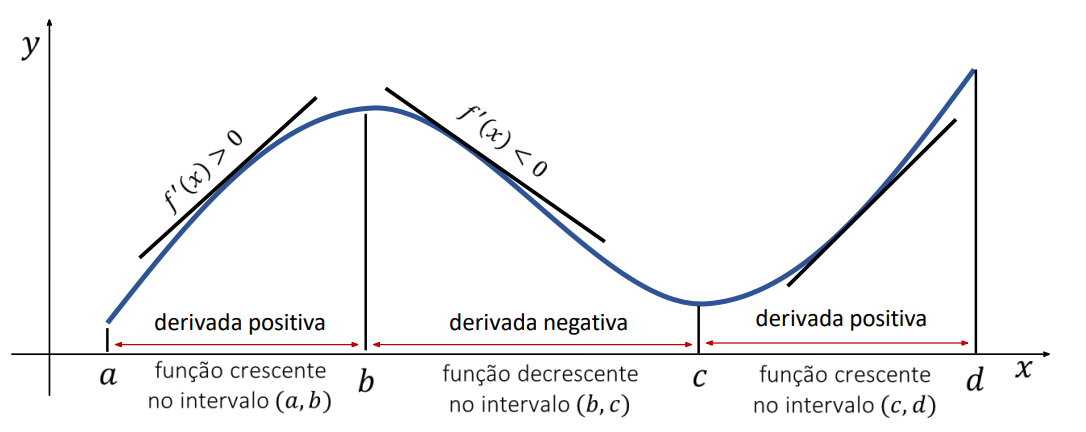
3) Exemplo Resolvido
Determine os intervalos de crescimento e decrescimento da função:
Ver solução passo a passo
Calculando a derivada:
Definindo o sinal de \(f'(x)\):
- Para \(f'(x) > 0\): \(2x – 2 > 0 \implies x > 1\). Intervalo crescente: \((1, +\infty)\).
- Para \(f'(x) < 0\): \(2x - 2 < 0 \implies x < 1\). Intervalo decrescente: \((-\infty, 1)\).
Portanto:
4) Continue estudando
Confira nossos guias para aprofundar seus conhecimentos sobre derivadas e aplicações:
Teste da Primeira Derivada — Exercícios com Soluções
Use a derivada \(f'(x)\) para identificar crescimento (\(f’>0\)), decrescimento (\(f’<0\)) e classificar os extremos locais via mudança de sinal. Cada questão inclui solução formatada com MathJax.
1) Parte Básica
-
Para \(f(x)=x^2-4x+3\), determine onde \(f\) é crescente/decrescente e identifique os extremos locais.
Ver solução
\[ f'(x)=2x-4 \] \[ f'(x)>0 \Longleftrightarrow x>2,\qquad f'(x)<0 \Longleftrightarrow x<2. \]Crescente: \((2,+\infty)\) | Decrescente: \((-\infty,2)\).\[ f(2)=2^2-4\cdot2+3=-1 \;\Rightarrow\; \text{mínimo local em }(2,-1). \] -
Para \(f(x)=-x^2+6x-5\), encontre os intervalos de crescimento/decrescimento e classifique o extremo.
Ver solução
\[ f'(x)=-2x+6,\qquad f'(x)=0 \Longleftrightarrow -2x+6=0 \Longrightarrow x=3. \] \[ f”(x)=-2<0 \;\Rightarrow\; \text{máximo local.} \]\[ f(3)=-(3)^2+6\cdot3-5=4 \;\Rightarrow\; \boxed{\text{máximo em }(3,4)}. \] -
Para \(f(x)=x^3-3x\), determine os intervalos de monotonicidade e os extremos locais.
Ver solução
\[ f'(x)=3x^2-3=3(x-1)(x+1). \]Sinais: \(+\) em \((-\infty,-1)\); \(−\) em \((-1,1)\); \(+\) em \((1,+\infty)\). Crescente: \((-\infty,-1)\cup(1,+\infty)\). Decrescente: \((-1,1)\).\[ f(-1)=2 \;(\,+\to-\,)\Rightarrow \text{máx. local}, \qquad f(1)=-2 \;(\,-\to+\,)\Rightarrow \text{mín. local}. \] -
Dada \(f(x)=e^x-2x\), encontre os intervalos de crescimento/decrescimento e classifique o ponto crítico.
Ver solução
\[ f'(x)=e^x-2=0 \Longleftrightarrow e^x=2 \Longrightarrow x=\ln2. \] \[ x<\ln2\Rightarrow f'(x)<0,\qquad x>\ln2\Rightarrow f'(x)>0. \]Decrescente: \((-\infty,\ln2)\) | Crescente: \((\ln2,+\infty)\).\[ f(\ln2)=2-2\ln2 \Rightarrow \boxed{\text{mínimo em }(\ln2,\,2-2\ln2)}. \] -
Para \(f(x)=\ln(x^2+1)\), determine crescimento/decrescimento e o extremo.
Ver solução
\[ f'(x)=\frac{2x}{x^2+1}. \]\(f'(x)<0\) se \(x<0\) e \(f'(x)>0\) se \(x>0\). Decrescente: \((-\infty,0)\) | Crescente: \((0,+\infty)\).\[ f(0)=\ln(1)=0 \Rightarrow \boxed{\text{mínimo em }(0,0)}. \]
2) Parte Intermediária
-
Para \(f(x)=x^3-6x^2+9x+2\):
(a) encontre os críticos; (b) indique \(\uparrow/\downarrow\); (c) calcule os valores dos extremos.
Ver solução
\[ f'(x)=3x^2-12x+9=3(x-1)(x-3). \]Críticos: \(x=1\) e \(x=3\). Sinais: \(+\) em \((-\infty,1)\), \(−\) em \((1,3)\), \(+\) em \((3,+\infty)\). Crescente: \((-\infty,1)\cup(3,+\infty)\). Decrescente: \((1,3)\).\[ f(1)=1-6+9+2=6 \quad(\text{máx.}), \qquad f(3)=27-54+27+2=2 \quad(\text{mín.}). \] -
Para \(f(x)=3x^4-8x^3+6\):
(a) calcule \(f'(x)\) e os críticos; (b) classifique; (c) verifique inflexão horizontal.
Ver solução
\[ f'(x)=12x^2(x-2). \]Críticos: \(x=0\) (raiz dupla) e \(x=2\). Sinais: \(f’<0\) para \(x<2\) (inclusive após atravessar \(0\)); \(f'>0\) para \(x>2\).\[ x=2:\; -\to+ \Rightarrow \text{mínimo},\quad f(2)=48-64+6=-10. \] \[ x=0:\; \text{sem troca de sinal} \Rightarrow \text{sem extremo (inflexão TH)}. \] -
Estude a monotonicidade de \(f(x)=\sqrt{x^2+4}-x\) em \(\mathbb{R}\) e conclua sobre extremos.
Ver solução
\[ f'(x)=\frac{x}{\sqrt{x^2+4}}-1. \]Como \(\displaystyle \left|\frac{x}{\sqrt{x^2+4}}\right|<1\) para todo \(x\), então \(f'(x)<0\). Decrescente em \(\mathbb{R}\) e sem extremos. -
Uma partícula move-se com \(s(t)=t^3-9t^2+24t\). Indique quando avança (\(v>0\)) e quando recua (\(v<0\)).
Ver solução
Velocidade:\[ v(t)=s'(t)=3t^2-18t+24=3(t-2)(t-4). \]Sinais: \(v>0\) em \((-\infty,2)\cup(4,+\infty)\) ⇒ **avança**; \(v<0\) em \((2,4)\) ⇒ **recuo**. -
Para \(f(x)=x\,e^{-x}\):
(a) ache os críticos; (b) intervalos \(\uparrow/\downarrow\); (c) valor do máximo local.
Ver solução
\[ f'(x)=e^{-x}(1-x)=0 \Longleftrightarrow x=1. \]Crescente: \((-\infty,1)\). Decrescente: \((1,+\infty)\).\[ f(1)=\frac{1}{e} \;\Rightarrow\; \boxed{\text{máximo em }(1,\,e^{-1})}. \]
3) Parte Avançada
-
Para \(f(x)=\dfrac{x^2}{x^2+1}\), determine crescimento/decrescimento e extremos; discuta \(\displaystyle\lim_{|x|\to\infty}f(x)\).
Ver solução
\[ f'(x)=\frac{2x}{(x^2+1)^2}. \]Decrescente: \((-\infty,0)\). Crescente: \((0,+\infty)\).\[ f(0)=0 \Rightarrow \text{mínimo em }(0,0),\qquad \lim_{x\to\pm\infty}f(x)=1 \;(\text{assíntota } y=1). \] -
Para \(f(x)=x-\ln(x+1)\) (domínio \(x>-1\)), estude \(\uparrow/\downarrow\) e o extremo.
Ver solução
\[ f'(x)=1-\frac{1}{x+1}=\frac{x}{x+1}. \]Denominador \(>0\) no domínio ⇒ sinal do numerador. Decrescente: \((-1,0)\); Crescente: \((0,+\infty)\).\[ f(0)=0 \Rightarrow \boxed{\text{mínimo em }(0,0)}. \] -
Para \(f(x)=\ln(x^2+4x+5)=\ln\!\big((x+2)^2+1\big)\), estude \(\uparrow/\downarrow\) e o extremo.
Ver solução
\[ f'(x)=\frac{2(x+2)}{(x+2)^2+1}. \]Decrescente: \((-\infty,-2)\); Crescente: \((-2,+\infty)\).\[ f(-2)=\ln 1=0 \Rightarrow \boxed{\text{mínimo em }(-2,0)}. \] -
Para \(f(x)=e^{2x}-3e^{x}\), encontre e classifique o crítico e calcule o valor no extremo.
Ver solução
\[ f'(x)=e^{x}(2e^{x}-3)=0 \;\Longleftrightarrow\; e^{x}=\frac{3}{2} \;\Longrightarrow\; x=\ln\!\frac{3}{2}. \] \[ f”(x)=e^x(4e^x-3)\Rightarrow f”\!\big(\ln\tfrac{3}{2}\big)=\tfrac{3}{2}(6-3)>0 \;\Rightarrow\; \text{mínimo}. \]Valor no extremo (use \(u=e^x=\tfrac{3}{2}\)):\[ f = u^2-3u = \frac{9}{4}-\frac{9}{2} = -\frac{9}{4}. \]Mínimo: \(\big(\ln\!\tfrac{3}{2},\,-\tfrac{9}{4}\big)\). \(\;f’<0\) se \(x<\ln\!\tfrac{3}{2}\) e \(f'>0\) se \(x>\ln\!\tfrac{3}{2}\). -
Para \(f(x)=\dfrac{x}{\sqrt{x^2+1}}\), prove que \(f'(x)>0\) para todo \(x\) e conclua a monotonicidade; discuta limites e imagem.
Ver solução
\[ f'(x)=\frac{1}{(x^2+1)^{3/2}} \;>\; 0 \quad \forall\,x\in\mathbb{R}. \]Logo, **crescente em \(\mathbb{R}\)**.\[ \lim_{x\to-\infty}f(x)=-1,\qquad \lim_{x\to+\infty}f(x)=1 \;\Rightarrow\; \text{imagem } (-1,1). \]
Resumo das respostas
Mostrar resumo
- Cresc.: \((2,\infty)\); Decr.: \((-\infty,2)\); mín.: \((2,-1)\).
- Máx.: \((3,4)\).
- Cresc.: \((-\infty,-1)\cup(1,\infty)\); Decr.: \((-1,1)\); máx.: \((-1,2)\); mín.: \((1,-2)\).
- Decr.: \((-\infty,\ln2)\); Cresc.: \((\ln2,\infty)\); mín.: \((\ln2,\,2-2\ln2)\).
- Decr.: \((-\infty,0)\); Cresc.: \((0,\infty)\); mín.: \((0,0)\).
- Cresc.: \((-\infty,1)\cup(3,\infty)\); Decr.: \((1,3)\); máx.: \(f(1)=6\); mín.: \(f(3)=2\).
- Mín.: \((2,-10)\); \(x=0\) sem extremo (inflexão TH).
- Decrescente em \(\mathbb{R}\); sem extremos.
- Avança: \((-\infty,2)\cup(4,\infty)\); Recua: \((2,4)\).
- Cresc.: \((-\infty,1)\); Decr.: \((1,\infty)\); máx.: \((1,\,e^{-1})\).
- Decr.: \((-\infty,0)\); Cresc.: \((0,\infty)\); mín.: \((0,0)\); \(\lim f=1\).
- Decr.: \((-1,0)\); Cresc.: \((0,\infty)\); mín.: \((0,0)\).
- Decr.: \((-\infty,-2)\); Cresc.: \((-2,\infty)\); mín.: \((-2,0)\).
- Mín.: \(\big(\ln\frac{3}{2},-\frac{9}{4}\big)\); sem máximo.
- Crescente em \(\mathbb{R}\); imagem: \((-1,1)\).
Links úteis
Dica: a mudança de sinal de \(f’\) decide a natureza do crítico: \(+\!\to\!-\) dá máximo; \(-\!\to\!+\) dá mínimo. Em dúvida, confirme com \(f”\).













