Máximos e Mínimos Locais — Teste da Primeira Derivada
Seja \(f\) derivável em um intervalo \(I\) e \(c\in I\) um ponto crítico de \(f\). Então:
\[
\begin{aligned}
&\text{Se } f’ \text{ muda de } + \text{ para } – \text{ em } c \Rightarrow \text{máximo local.}\\
&\text{Se } f’ \text{ muda de } – \text{ para } + \text{ em } c \Rightarrow \text{mínimo local.}\\
&\text{Se } f’ \text{ não muda de sinal em } c \Rightarrow \text{nem máximo nem mínimo.}
\end{aligned}
\]
1) Intuição visual
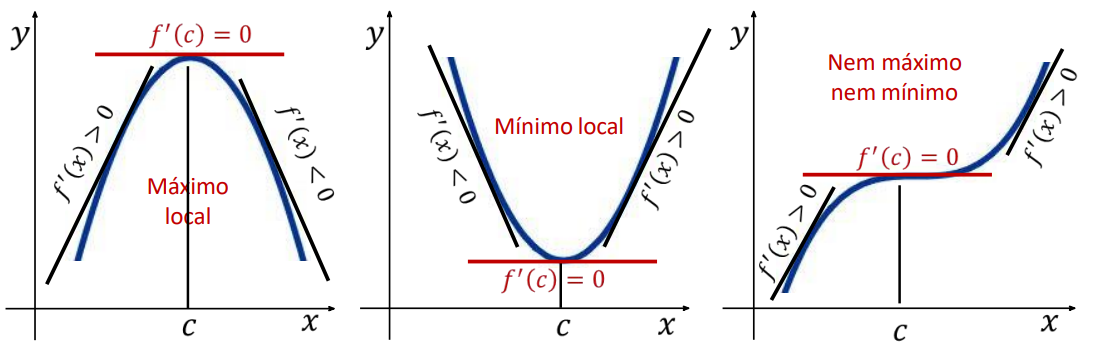
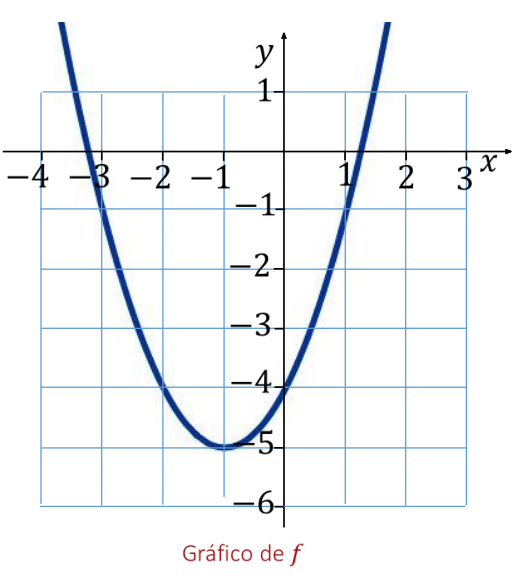
Tabela de sinais do exemplo resolvido (f(x)=x²+2x−4)
| Intervalo | \(f'(x)=2x+2\) | Comportamento de \(f\) |
|---|---|---|
| \((-\infty,-1)\) | − | Decrescente |
| \(x=-1\) | 0 | Mínimo local |
| \((-1,\infty)\) | + | Crescente |
2) Exemplos resolvidos
Exemplo A — Exponencial menos linear
\(f(x)=e^x-2x\). Classifique o ponto crítico e calcule \(f(c)\).
Ver solução + tabela de sinais
\[
f'(x)=e^x-2=0 \Rightarrow c=\ln2.
\]
| Intervalo | \(f'(x)\) | Comportamento |
|---|---|---|
| \((-\infty,\ln2)\) | − | Decrescente |
| \(x=\ln2\) | 0 | Mínimo local |
| \((\ln2,\infty)\) | + | Crescente |
\[
f(\ln2)=2-2\ln2.
\]
Exemplo B — Racional
\(f(x)=\dfrac{x^2}{x-1}\). Encontre e classifique os extremos locais.
Ver solução + tabela de sinais
\[
f'(x)=\frac{x(x-2)}{(x-1)^2} \Rightarrow \text{críticos } x=0,\,2;\ \ x=1\ \text{fora do domínio}.
\]
| Intervalo | \(f'(x)\) | Comportamento |
|---|---|---|
| \((-\infty,0)\) | + | Crescente |
| \(x=0\) | 0 | Máximo local |
| \((0,1)\) | − | Decrescente |
| \(x=1\) | — | sem definição |
| \((1,2)\) | − | Decrescente |
| \(x=2\) | 0 | Mínimo local |
| \((2,\infty)\) | + | Crescente |
\[
f(0)=0, \qquad f(2)=4.
\]
3) Exercícios propostos (com solução e tabela de sinais)
-
\(f(x)=x^3-3x\). Localize e classifique todos os extremos locais.
Mostrar solução + sinais
\[ f'(x)=3(x-1)(x+1). \]Intervalo \(f'(x)\) Comportamento \((-\infty,-1)\) + Crescente \(x=-1\) 0 Máximo local \((-1,1)\) − Decrescente \(x=1\) 0 Mínimo local \((1,\infty)\) + Crescente \[ f(-1)=2,\quad f(1)=-2. \] -
\(f(x)=x\,e^{-x}\). Determine o crítico e mostre que é máximo.
Mostrar solução + sinais
\[ f'(x)=e^{-x}(1-x)=0 \Rightarrow x=1. \]Intervalo \(f'(x)\) Comportamento \((-\infty,1)\) + Crescente \(x=1\) 0 Máximo local \((1,\infty)\) − Decrescente \[ f(1)=e^{-1}. \] -
\(f(x)=\ln x – x\) (domínio \(x>0\)). Classifique via teste da 1ª derivada.
Mostrar solução + sinais
\[ f'(x)=\frac{1}{x}-1=0 \Rightarrow x=1. \]Intervalo \(f'(x)\) Comportamento \((0,1)\) + Crescente \(x=1\) 0 Máximo local \((1,\infty)\) − Decrescente \[ f(1)=-1. \] -
\(f(x)=\dfrac{x}{\sqrt{x^2+1}}\). Mostre que não há extremos.
Mostrar solução + sinais
\[ f'(x)=\frac{1}{(x^2+1)^{3/2}}>0\ \forall x. \]Intervalo \(f'(x)\) Comportamento \((-\infty,\infty)\) + Estritamente crescente (sem críticos) -
\(f(x)=x^4-4x^2\). Encontre e classifique os extremos.
Mostrar solução + sinais
\[ f'(x)=4x(x^2-2)=0 \Rightarrow x=0,\ \pm\sqrt2. \]Intervalo \(f'(x)\) Comportamento \((-\infty,-\sqrt2)\) − Decrescente \(x=-\sqrt2\) 0 Mínimo local \((-\sqrt2,0)\) + Crescente \(x=0\) 0 Máximo local \((0,\sqrt2)\) − Decrescente \(x=\sqrt2\) 0 Mínimo local \((\sqrt2,\infty)\) + Crescente \[ f(0)=0,\qquad f(\pm\sqrt2)=-4. \]
4) Resumo rápido
Regra de ouro: mudança \(+\to-\) dá máximo; mudança \(-\to+\) dá mínimo; sem mudança ⇒ não é extremo.













