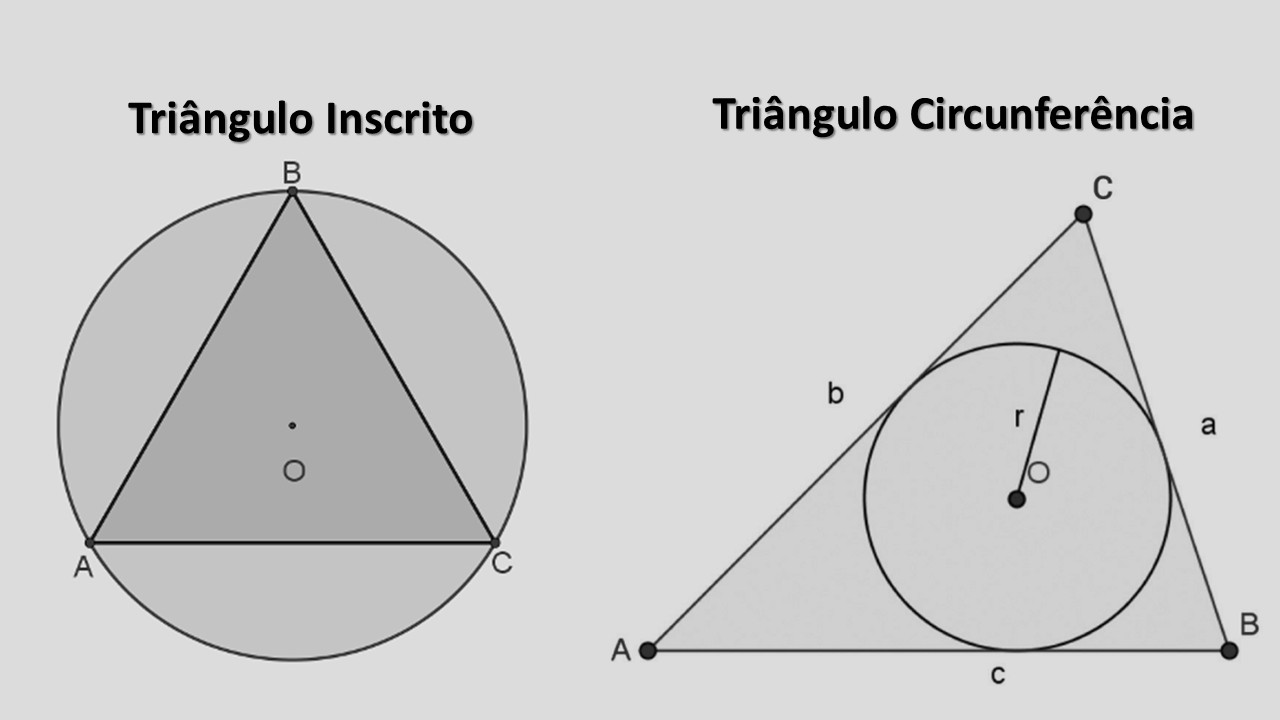
Triângulo Inscrito na Circunferência (Triângulo Cíclico)
SEO discreto: termos como “triângulo inscrito na circunferência”, “circuncentro”, “incírculo”, “raio \(R\)” e “raio \(r\)” aparecem naturalmente no texto.
Definição
Um triângulo inscrito (ou triângulo cíclico) é aquele cujos três vértices pertencem à mesma circunferência, chamada circunferência circunscrita. O centro dessa circunferência é o circuncentro \(O\) e o seu raio é \(R\). O circuncentro é a interseção das mediatrizes dos lados do triângulo.
A posição de \(O\) varia com a classe por ângulos: fica dentro no acutângulo, no ponto médio da hipotenusa no retângulo e fora no obtusângulo. Revise: acutângulo, retângulo e obtusângulo.
Figuras principais

Triângulo Circunferência
Usaremos “Triângulo Circunferência” para destacar a situação em que um círculo está inscrito no triângulo (incírculo). O centro é o incentro — interseção das bissetrizes internas — e o raio é \(r\). A área relaciona-se ao semiperímetro \(s=\tfrac{a+b+c}{2}\) por \(A=rs\). Combinar esta fórmula com Heron \(A=\sqrt{s(s-a)(s-b)(s-c)}\) permite obter \(r\) a partir dos lados. Detalhes dos centros em Pontos Notáveis do Triângulo.
Triângulo Inscrito
No Triângulo Inscrito (ou cíclico), os vértices \(A,B,C\) estão sobre a circunferência de raio \(R\) e centro \(O\) (circuncentro). Valem a Lei dos Senos estendida \(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\) e a área por \(R\) \(A=\dfrac{abc}{4R}\) . Caso especial (Teorema de Tales): se um lado é diâmetro da circunferência circunscrita, o ângulo oposto é reto.
Propriedades adicionais e fórmulas
Ângulos na circunferência
- Ângulo inscrito mede metade do ângulo central correspondente.
- Ângulos inscritos que subtendem o mesmo arco são congruentes.
- Se um lado é diâmetro, o ângulo oposto é \(90^\circ\) (caso retângulo).
Resumo de fórmulas (uma por linha)
Classificação por lados: equilátero, isósceles, escaleno. Área geral em Área de Triângulo.
Exemplos resolvidos (passo a passo vertical)
Exemplo 1 — Num triângulo inscrito, \(a=10\) e \(A=60^\circ\). Calcule \(R\).
Mostrar solução
\(2R=\dfrac{a}{\sin A}\)
\(=\dfrac{10}{\sin 60^\circ}\)
\(=\dfrac{10}{\frac{\sqrt3}{2}}\)
\(=\dfrac{20}{\sqrt3}\Rightarrow R=\dfrac{10}{\sqrt3}=\dfrac{10\sqrt3}{3}\approx 5{,}77\).
Exemplo 2 — Um triângulo tem lados \(7,8,9\). Encontre \(R\).
Mostrar solução
\(s=\dfrac{7+8+9}{2}\)
\(=12\)
\(A=\sqrt{12(12-7)(12-8)(12-9)}\)
\(=\sqrt{12\cdot 5\cdot 4\cdot 3}\)
\(=12\sqrt{5}\)
\(R=\dfrac{abc}{4A}\)
\(=\dfrac{7\cdot 8\cdot 9}{4\cdot 12\sqrt5}\)
\(=\dfrac{504}{48\sqrt5}\)
\(=\dfrac{10{,}5}{\sqrt5}=\dfrac{10{,}5\sqrt5}{5}\approx 4{,}69\).
Exemplo 3 — O incírculo tem \(r=4\) e \(s=15\). Calcule a área.
Mostrar solução
\(A=rs\)
\(=4\cdot 15\)
\(=60\).
Exercícios de múltipla escolha (com solução em abre/fecha)
1) No triângulo inscrito \(ABC\), \(a=12\) e \(A=30^\circ\). O raio \(R\) vale:
Mostrar solução
\(2R=\dfrac{a}{\sin A}\)
\(=\dfrac{12}{\sin30^\circ}\)
\(=\dfrac{12}{\tfrac12}\)
\(=24\Rightarrow R=12\).
2) Se um lado do triângulo inscrito é um diâmetro da circunferência, então o triângulo é:
Mostrar solução
Teorema de Tales: o ângulo oposto ao diâmetro é \(90^\circ\). Alternativa C.
3) Dado \(a=8\), \(b=10\), \(c=12\) e \(A= \arcsin\!\left(\dfrac{a}{2R}\right)\). O valor de \(2R\) é:
Mostrar solução
Lei dos senos estendida: \( \dfrac{a}{\sin A}=2R \). Alternativa D.
4) Um triângulo tem \(s=18\) e \(r=3\). Sua área é:
Mostrar solução
\(A=rs\)
\(=3\cdot 18\)
\(=54\).
5) Para lados \(7,8,9\), a área é \(12\sqrt5\). Então \(R\) é (aprox.):
Mostrar solução
\(R=\dfrac{abc}{4A}\)
\(=\dfrac{504}{48\sqrt5}\)
\(=\dfrac{10{,}5}{\sqrt5}\approx 4{,}69\).
6) Em um triângulo inscrito, qual afirmação é sempre verdadeira?
Mostrar solução
Lei dos senos (proporção básica) vale para todo triângulo. Correta: C.
7) Se \(A=90^\circ\) e o triângulo é inscrito, então:
Mostrar solução
Ângulo reto subtende um diâmetro. O lado oposto a \(A\) é \(BC\) ⇒ diâmetro. Alternativa C.
8) Se \(R=5\) e \(A=30^\circ\), então o lado oposto a \(A\) vale:
Mostrar solução
\(a=2R\sin A\)
\(=2\cdot 5\cdot \sin30^\circ\)
\(=10\cdot \tfrac12\)
\(=5\).
9) Dado \(a=12\), \(b=13\), \(c=5\). Se \(A=\arccos\!\left(\dfrac{b^2+c^2-a^2}{2bc}\right)\), então \(2R\) é:
Mostrar solução
Lei dos senos estendida: \(2R=\dfrac{a}{\sin A}\). Alternativa D.
10) O incírculo de um triângulo tem \(r=2\) e \(s=21\). A área é:
Mostrar solução
\(A=rs\)
\(=2\cdot 21\)
\(=42\).
Continue estudando
Tipos de Triângulos Triângulo equilátero Triângulo isósceles Triângulo escaleno Triângulo retângulo Triângulo acutângulo Triângulo obtusângulo Área de triângulo Pontos notáveis