Questão 12 – ENEM/MEC
Ao morrer, o pai de João, Pedro e José deixou como herança um terreno retangular de 3 km × 2 km, que contém uma área de extração de ouro delimitada por um quarto de círculo de raio \( 1 \, \text{km} \) a partir do canto inferior esquerdo da propriedade. Dado o maior valor da área de extração de ouro, os irmãos acordaram em repartir a propriedade de modo que cada um ficasse com a terça parte da área de extração, conforme mostra a figura.
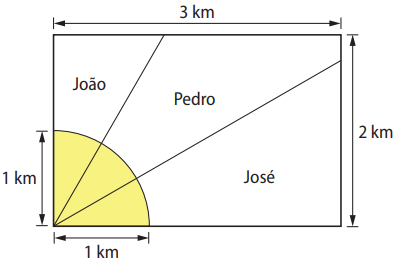
Em relação à partilha proposta, qual é a porcentagem aproximada da área do terreno que coube a João?
- a) 50%
- b) 43%
- c) 37%
- d) 33%
- e) 19%
Solução Passo a Passo:
O terreno total possui área: \[ A_{total} = 3 \cdot 2 = 6 \, \text{km}^2. \]
A área do setor circular é: \[ A_{setor} = \frac{\pi \cdot 1^2}{4} = \frac{\pi}{4} \, \text{km}^2. \]
Como João ficou com um terço da área de extração: \[ A_{João,setor} = \frac{1}{3} \cdot \frac{\pi}{4} = \frac{\pi}{12} \, \text{km}^2. \]
Considerando a parte do terreno de João, a área aproximada (calculada com base na divisão do setor) é: \[ A_{João} \approx \frac{2 \sqrt{3}}{3} \, \text{km}^2. \]
A porcentagem da área de João em relação ao terreno total é: \[ P_{João} = \frac{A_{João}}{A_{total}} \cdot 100 = \frac{\frac{2 \sqrt{3}}{3}}{6} \cdot 100 = \frac{\sqrt{3}}{9} \cdot 100 \approx 19\%. \]
Resposta: alternativa e) 19%.
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon