UNICAMP 2020 – Colinearidade e Distâncias no Gráfico de y=√x
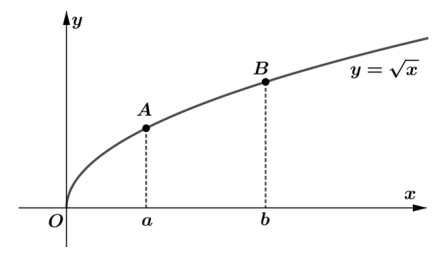
A figura abaixo exibe, no plano cartesiano, o gráfico de \( y = \sqrt{x} \) para \( x \ge 0 \),
em que os pontos \( A \) e \( B \) têm abscissas \( x_A = a > 0 \) e \( x_B = b > a \),
e \( C \) é a origem do sistema de coordenadas.
a) Prove que os pontos \( A, B \) e \( C = (-\sqrt{ab}, 0) \) são colineares. b) Para \( b = 3 \), determine o valor de \( a \) para o qual a distância da origem ao ponto \( A \) é igual à distância do ponto \( A \) ao ponto \( B \).

a) Prove que os pontos \( A, B \) e \( C = (-\sqrt{ab}, 0) \) são colineares. b) Para \( b = 3 \), determine o valor de \( a \) para o qual a distância da origem ao ponto \( A \) é igual à distância do ponto \( A \) ao ponto \( B \).
- Provar a colinearidade de A, B e C:
Para três pontos serem colineares, o determinante da matriz formada por suas coordenadas homogêneas deve ser zero: \[ \begin{vmatrix} a & \sqrt{a} & 1 \\ b & \sqrt{b} & 1 \\ -\sqrt{ab} & 0 & 1 \end{vmatrix} = 0 \] Expansão do determinante: \[ a\sqrt{b} + (-\sqrt{ab}) \cdot 1 + \sqrt{ab} – b\sqrt{a} = 0 \] \[ a\sqrt{b} – b\sqrt{a} = 0 \quad \Rightarrow \quad \sqrt{a}(\sqrt{a}\sqrt{b} – \sqrt{b}\sqrt{a}) = 0 \] Logo, \( A, B \) e \( C \) são colineares. - Determinando a distância (\( b = 3 \)):
Igualamos \( d_{A,O} = d_{B,A} \): \[ x_A^2 + y_A^2 = (x_B – x_A)^2 + (y_B – y_A)^2 \] \[ a + a = (3-a)^2 + (\sqrt{3} – \sqrt{a})^2 \] Resolvendo, obtemos: \[ a = \frac{4}{3}, \quad \sqrt{a} = \frac{2\sqrt{3}}{3} \]
Respostas:
- a) Demonstração da colinearidade
- b) \( A = \left(\frac{4}{3}, \frac{2\sqrt{3}}{3}\right) \)
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:

























