a) Supondo que \( ABC \) é um triângulo retângulo com perímetro igual a 16 cm e hipotenusa de comprimento 7 cm, calcule sua área.
b) Sabendo que, em um triângulo qualquer, a soma dos comprimentos de quaisquer dois lados é sempre maior que o comprimento do terceiro lado e assumindo que as medidas dos lados de um certo triângulo são \( a \), \( a^2 \) e \( a^3 \), calcule os possíveis valores de \( a \).
a) Área do triângulo retângulo:
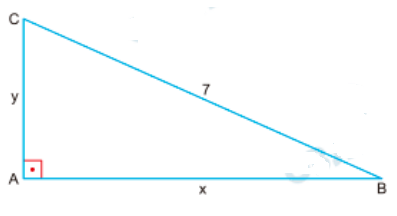
- Sabemos que \( x + y + 7 = 16 \Rightarrow x + y = 9 \).
- Pelo Teorema de Pitágoras: \( x^2 + y^2 = 7^2 = 49 \).
- Usando \( (x+y)^2 = x^2 + 2xy + y^2 = 81 \):
Área \( A = \frac{x \cdot y}{2} = \frac{16}{2} = 8 \text{ cm}^2 \).
b) Lados do triângulo: \( a \), \( a^2 \), \( a^3 \).
- Maior lado < soma dos outros dois:
Para \( 0 < a < 1 \): maior lado é \( a \)
\[ a^3 + a^2 > a \quad \Rightarrow \quad a(a^2 + a – 1) > 0 \]Para \( a > 1 \): maior lado é \( a^3 \)
\[ a^3 < a + a^2 \quad \Rightarrow \quad a^3 - a^2 - a < 0 \]Simplificando, os valores possíveis de \( a \) são:
\[ \frac{-1+\sqrt{5}}{2} < a < 1 \quad \text{ou} \quad 1 < a < \frac{1+\sqrt{5}}{2} \]Resposta final:
- a) \( 8 \text{ cm}^2 \)
- b) \( \frac{-1+\sqrt{5}}{2} < a < 1 \) ou \( 1 < a < \frac{1+\sqrt{5}}{2} \)
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:

























