Triângulo Retângulo

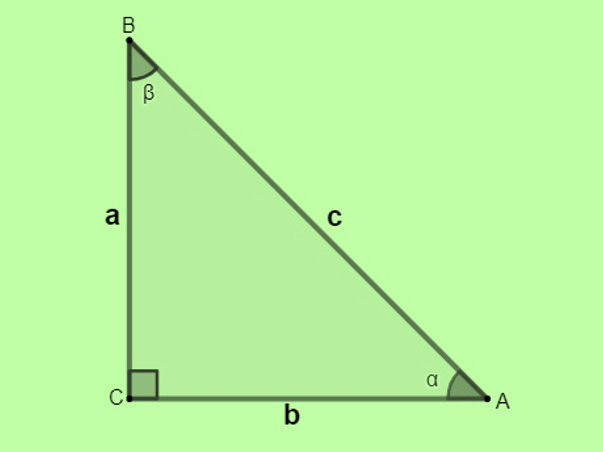
O triângulo retângulo possui um ângulo interno de \(90^\circ\). Os lados que formam o ângulo reto são os catetos (\(a\) e \(b\)); o lado oposto é a hipotenusa (\(c\)). Este tipo é central na Geometria e na Trigonometria.

Leituras relacionadas: Área de Triângulo · Lei dos Senos · Lei do Cosseno · Tipos de Triângulos.

Teorema de Pitágoras

\[ \boxed{a^2 + b^2 = c^2} \]

Válido apenas para triângulos retângulos. O converso do teorema classifica triângulos usando o maior lado \(c\): \(a^2+b^2=c^2\Rightarrow\) retângulo; \(a^2+b^2>c^2\Rightarrow\) acutângulo; \(a^2+b^2

Relações métricas na hipotenusa

Triângulo retângulo: \(\alpha+\beta=90^\circ\), hipotenusa \(c\), catetos \(a\) e \(b\).

Se a altura do vértice do ângulo reto até a hipotenusa é \(h\), e as projeções dos catetos sobre a hipotenusa são \(m\) (do cateto \(a\)) e \(n\) (do cateto \(b\)), então \(m+n=c\) e:

\[ \boxed{\textbf{Pitágoras:}\quad a^2=b^2+c^2} \]

\[ \boxed{\textbf{Decomposição da hipotenusa:}\quad a=m+n} \]

\[ \boxed{c^2=a\,m} \]

\[ \boxed{b^2=a\,n} \]

\[ \boxed{h^2=m\,n} \]

\[ \boxed{b\,c=a\,h} \]

\[ \boxed{c\,h=b\,m} \]

\[ \boxed{b\,h=c\,n} \]

Observação: estas igualdades decorrem de semelhança dos triângulos formados pela altura \(h\) na hipotenusa.

Exemplo rápido — encontre \(b\), \(c\) e \(h\)

Sabendo que \(a=20\ \text{cm}\), \(m=8\ \text{cm}\) e \(n=12\ \text{cm}\), calcule \(b\), \(c\) e \(h\).

Ver solução

\[ \begin{aligned} a &= m+n = 8+12 = 20\ (\checkmark)\\[2pt] c^2 &= a\,m = 20\cdot 8 = 160 \ \Rightarrow\ c=4\sqrt{10}\ \text{cm}\\[2pt] b^2 &= a\,n = 20\cdot 12 = 240 \ \Rightarrow\ b=4\sqrt{15}\ \text{cm}\\[2pt] h^2 &= m\,n = 8\cdot 12 = 96 \ \Rightarrow\ h=4\sqrt{6}\ \text{cm}\\[2pt] \text{cheque: } &\ b\,c = (4\sqrt{15})(4\sqrt{10})=16\sqrt{150}=16\cdot 5\sqrt{6}=80\sqrt{6}\\ & a\,h = 20\cdot (4\sqrt{6})=80\sqrt{6}\quad (\checkmark) \end{aligned} \]

Razões trigonométricas (ângulos agudos)

Com \(\alpha\) em \(A\) e \(\beta\) em \(B\):

\[ \boxed{\sin\alpha=\tfrac{a}{c}} \]

\[ \boxed{\cos\alpha=\tfrac{b}{c}} \]

\[ \boxed{\tan\alpha=\tfrac{a}{b}} \]

\[ \boxed{\sin\beta=\tfrac{b}{c}} \]

\[ \boxed{\cos\beta=\tfrac{a}{c}} \]

\[ \boxed{\tan\beta=\tfrac{b}{a}} \]

\[ \boxed{\alpha+\beta=90^\circ} \]

Ângulos notáveis \(30^\circ\!-\!60^\circ\!-\!90^\circ\) → lados proporcionais a \(1:\sqrt{3}:2\). Isósceles retângulo \(45^\circ\!-\!45^\circ\!-\!90^\circ\) → catetos iguais e \(c=a\sqrt{2}\).

Área, perímetro e círculos notáveis

\[ \boxed{A=\tfrac{a\,b}{2}} \]

\[ \boxed{P=a+b+c} \]

\[ \boxed{h=\tfrac{a\,b}{c}} \quad(\text{altura na hipotenusa}) \]

\[ \boxed{r=\tfrac{A}{s}} \]

\[ \boxed{r=\tfrac{a+b-c}{2}} \quad(\text{fórmula específica para triângulo retângulo}) \]

\[ \boxed{R=\tfrac{c}{2}} \quad(\text{circuncentro é o ponto médio da hipotenusa}) \]

Exemplos resolvidos

Exemplo 1 — Pitágoras + área + perímetro

Num triângulo retângulo, os catetos valem \(a=6\,\text{cm}\) e \(b=8\,\text{cm}\). Calcule \(c\), a área e o perímetro.

Ver solução

\[ \begin{aligned} c^2 &= a^2+b^2\\ &= 6^2+8^2\\ &= 36+64\\ &= 100\\ c &= 10\\[6pt] A &= \frac{a\cdot b}{2}\\ &= \frac{6\cdot 8}{2}\\ &= 24\ \text{cm}^2\\[6pt] P &= a+b+c\\ &= 6+8+10\\ &= \boxed{24\ \text{cm}} \end{aligned} \]

Exemplo 2 — hipotenusa dada, ache o cateto e os ângulos

Dado \(c=13\,\text{cm}\) e um cateto \(a=5\,\text{cm}\). Encontre \(b\), \(\alpha\) (oposto a \(a\)) e \(\beta\).

Ver solução

\[ \begin{aligned} b^2 &= c^2-a^2\\ &= 13^2-5^2\\ &= 169-25\\ &= 144\\ b &= 12\\[6pt] \sin\alpha &= \frac{a}{c}\\ &= \frac{5}{13}\\ \alpha &\approx 22{,}62^\circ\\[6pt] \beta &= 90^\circ-\alpha\\ &\approx 67{,}38^\circ \end{aligned} \]

Exemplo 3 — lado e ângulo \(\Rightarrow\) complete o triângulo

Com hipotenusa \(c=10\,\text{cm}\) e \(\alpha=30^\circ\), determine \(a\) (oposto a \(\alpha\)) e \(b\).

Ver solução

\[ \begin{aligned} a &= c\sin\alpha\\ &= 10\sin 30^\circ\\ &= 10\cdot 0{,}5\\ &= 5\\[6pt] b &= c\cos\alpha\\ &= 10\cos 30^\circ\\ &= 10\cdot \frac{\sqrt{3}}{2}\\ &= \boxed{5\sqrt{3}\ \text{cm}\ (\approx 8{,}66)} \end{aligned} \]

Exemplo 4 — relações métricas na hipotenusa

Na figura, \(c=20\,\text{cm}\) e a projeção do cateto \(a\) vale \(m=8\,\text{cm}\). Encontre \(a\), \(b\), \(h\) e \(n\).

Ver solução

\[ \begin{aligned} a^2 &= c\,m = 20\cdot 8 = 160 \Rightarrow a=4\sqrt{10}\\[4pt] n &= c-m = 20-8 = 12\\[4pt] b^2 &= c\,n = 20\cdot 12 = 240 \Rightarrow b=4\sqrt{15}\\[4pt] h^2 &= m\,n = 8\cdot 12 = 96 \Rightarrow h=4\sqrt{6} \end{aligned} \]

Exercícios (múltipla escolha)

(1)

Num triângulo retângulo, \(a=9\) e \(b=12\) (cm). A hipotenusa mede:

Mostrar solução

\(c=\sqrt{9^2+12^2}=\sqrt{81+144}=\sqrt{225}=15\). Resp.: B.

(2)

Com \(c=26\) e \(a=10\) (cm), o outro cateto vale:

Mostrar solução

\(b=\sqrt{26^2-10^2}=\sqrt{676-100}=\sqrt{576}=24\). Resp.: E.

(3)

Se \(a=7\) cm, \(c=25\) cm, então \(\alpha\) (oposto a \(a\)) é aproximadamente:

\(14^\circ\)
\(16^\circ\)
\(18^\circ\)
\(20^\circ\)
\(22^\circ\)

Mostrar solução

\(\sin\alpha=\tfrac{7}{25}=0{,}28\Rightarrow \alpha\approx 16{,}26^\circ\). Resp.: B.

(4)

Num isósceles retângulo com cateto \(x\), a hipotenusa é:

\(x\)
\(x\sqrt{2}\)
\(2x\)
\(x\sqrt{3}\)
\(x/2\)

Mostrar solução

Razão \(45^\circ\!-\!45^\circ\!-\!90^\circ\): \(c=x\sqrt{2}\). Resp.: B.

(5)

Se \(a=15\) cm, \(b=20\) cm, então a altura na hipotenusa é:

Mostrar solução

\(h=\dfrac{a\,b}{c}\), com \(c=\sqrt{15^2+20^2}=25\). Logo, \(h=\dfrac{15\cdot 20}{25}=12\). Resp.: C.

Resumo rápido (uma por linha)

\[ \textbf{Pitágoras:}\quad a^2+b^2=c^2 \]

\[ \textbf{Soma dos ângulos agudos:}\quad \alpha+\beta=90^\circ \]

\[ \textbf{Área:}\quad A=\frac{a\,b}{2} \]

\[ \textbf{Perímetro:}\quad P=a+b+c \]

\[ \textbf{Altura na hipotenusa:}\quad h=\frac{a\,b}{c} \]

\[ \textbf{Inraio (geral):}\quad r=\frac{A}{s} \quad (s=\tfrac{a+b+c}{2}) \]

\[ \textbf{Inraio (retângulo):}\quad r=\frac{a+b-c}{2}=\frac{a\,b}{a+b+c} \]

\[ \textbf{Circunrádio:}\quad R=\frac{c}{2} \]

\[ \textbf{Métricas:}\quad a^2=c\,m \]

\[ \textbf{Métricas:}\quad b^2=c\,n \]

\[ \textbf{Métricas:}\quad h^2=m\,n \]

\[ \textbf{Métricas:}\quad a\,b=c\,h \]

\[ \textbf{Trigonometria:}\quad \sin\alpha=\tfrac{a}{c},\ \cos\alpha=\tfrac{b}{c},\ \tan\alpha=\tfrac{a}{b} \]

\[ \textbf{Trigonometria:}\quad \sin\beta=\tfrac{b}{c},\ \cos\beta=\tfrac{a}{c},\ \tan\beta=\tfrac{b}{a} \]

Continue estudando: Área de Triângulo · Lei dos Senos · Lei do Cosseno.

Triângulo Retângulo

Triângulo Retângulo

Teorema de Pitágoras

Relações métricas na hipotenusa

Exemplo rápido — encontre \(b\), \(c\) e \(h\)

Razões trigonométricas (ângulos agudos)

Área, perímetro e círculos notáveis

Exemplos resolvidos

Exemplo 1 — Pitágoras + área + perímetro

Exemplo 2 — hipotenusa dada, ache o cateto e os ângulos

Exemplo 3 — lado e ângulo \(\Rightarrow\) complete o triângulo

Exemplo 4 — relações métricas na hipotenusa

Exercícios (múltipla escolha)

(1)

(2)

(3)

(4)

(5)

Resumo rápido (uma por linha)

Materiais do Matemática Hoje

Área Polígono regular

Áreas do Retângulo

Área do Quadrado

"Artigo escrito por"

Adriano Rocha

Nos ajude compartilhando esse post 😉

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Desigualdade Triangular

Triângulo Escaleno

Área de Triângulo

Triângulo Equilátero

Triângulo Retângulo

Tipo de Triângulos

📘 Baixe Grátis o eBook de Fórmulas Matemática

📘 Mapas Mentais

📚 10 E-books de Matemática

Questões

Conteúdo

Banca