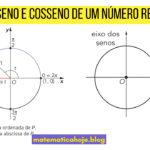
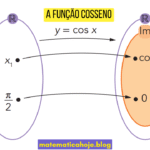
Como aprender seno e cosseno com a mão?
A trigonometria é uma das áreas mais fascinantes da matemática, mas muitos estudantes têm dificuldade em decorar os valores de seno e cosseno dos principais ângulos. Pensando nisso, existe um método visual e extremamente prático: usar a própria mão como guia! Com essa técnica, você memoriza os valores de sen(φ) e cos(φ) de forma rápida e divertida, sem depender de tabelas.
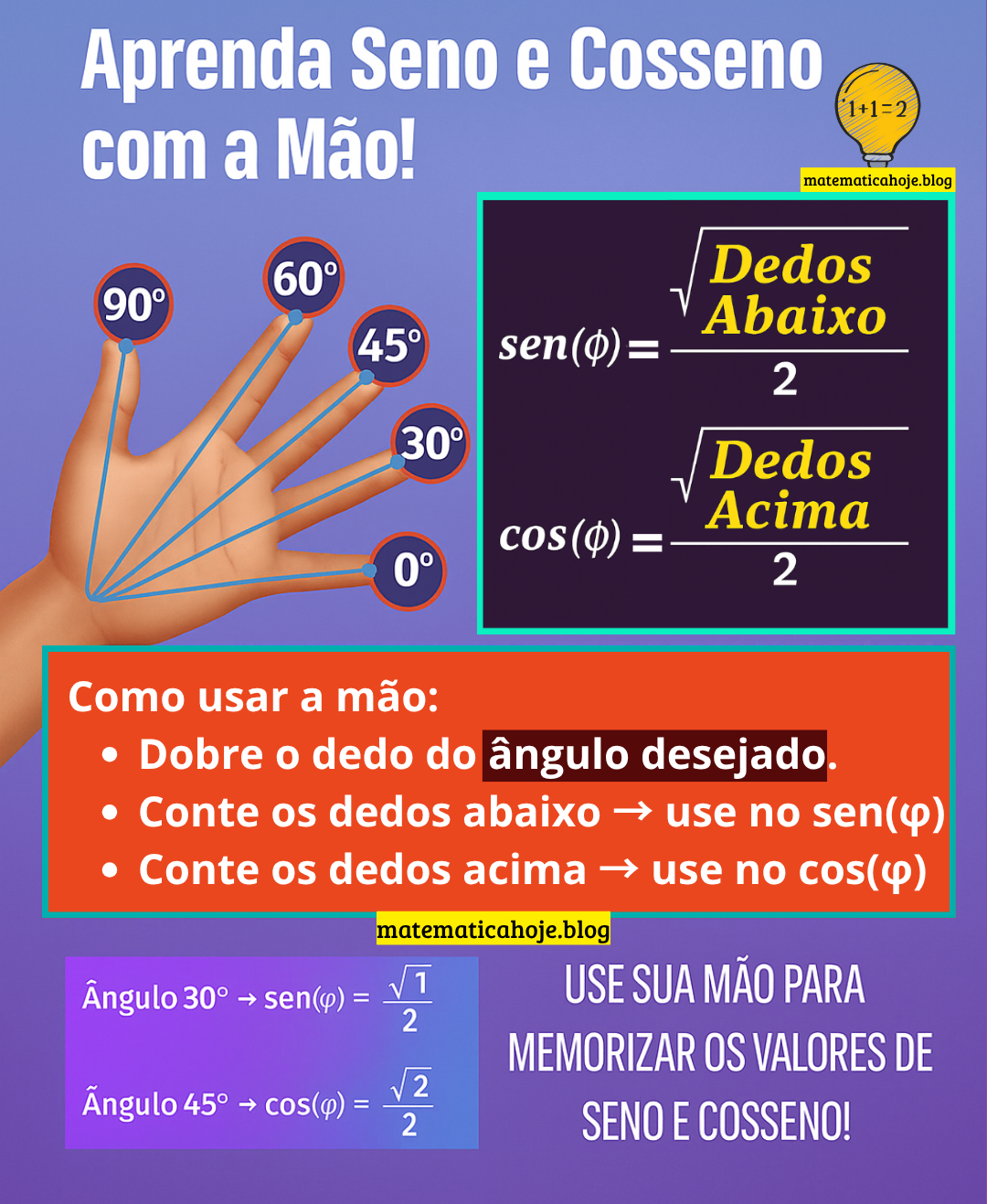
Como funciona o método da mão na trigonometria
Observe sua mão esquerda aberta. Cada dedo representa um ângulo especial:
- Polegar → 0°
- Indicador → 30°
- Médio → 45°
- Anelar → 60°
- Mínimo → 90°
Para encontrar o valor de seno e cosseno de um ângulo, siga:
- Dobre o dedo que representa o ângulo desejado.
- Conte os dedos abaixo → use na fórmula do seno.
- Conte os dedos acima → use na fórmula do cosseno.
Fórmulas:
$$\sin(\phi)=\frac{\sqrt{\text{dedos abaixo}}}{2}\qquad \cos(\phi)=\frac{\sqrt{\text{dedos acima}}}{2}$$
Exemplos práticos: aprendendo com a mão
Exemplo 1 — Calculando sen(30°)
Ao dobrar o dedo do ângulo de 30°, há 1 dedo abaixo.
$$\sin(30^\circ)=\frac{\sqrt{1}}{2}=\frac{1}{2}$$
Exemplo 2 — Calculando cos(45°)
Ao dobrar o dedo do ângulo de 45°, há 2 dedos acima.
$$\cos(45^\circ)=\frac{\sqrt{2}}{2}$$
Método prático para a tangente com a mão
A tangente pode ser obtida sem nova decoração usando os mesmos dedos. Basta lembrar que:
$$\tan(\phi)=\frac{\sin(\phi)}{\cos(\phi)}=\frac{\sqrt{\text{abaixo}}}{\sqrt{\text{acima}}} =\sqrt{\frac{\text{abaixo}}{\text{acima}}}$$
| Ângulo | Dedos abaixo | Dedos acima | \(\tan(\phi)\) |
|---|---|---|---|
| 0° | 0 | 5 | \(0\) |
| 30° | 1 | 3 | \(\sqrt{\frac{1}{3}}=\frac{\sqrt{3}}{3}\) |
| 45° | 2 | 2 | \(\sqrt{\frac{2}{2}}=1\) |
| 60° | 3 | 1 | \(\sqrt{\frac{3}{1}}=\sqrt{3}\) |
| 90° | 5 | 0 | indefinida |
Exemplo rápido — \(\tan(60^\circ)\)
Dobre o dedo do 60°. Abaixo = 3, acima = 1.
$$\tan(60^\circ)=\sqrt{\frac{3}{1}}=\sqrt{3}$$
Por que esse método é tão eficiente?
O uso da mão como ferramenta de memorização estimula o aprendizado visual e tátil. Isso ajuda a criar uma associação física entre os ângulos e seus valores trigonométricos. Além disso, é uma maneira prática e divertida de revisar fórmulas antes de provas ou concursos, sem precisar de calculadora.
Lista de exercícios resolvidos sobre seno, cosseno e tangente
Questão 1 — Seno de 60°
(Fundamental) Usando o método da mão, determine \( \sin(60^\circ) \).
👀 Ver solução passo a passo
60° → abaixo = 3.
$$\sin(60^\circ)=\frac{\sqrt{3}}{2}$$
Questão 2 — Cosseno de 30°
(Médio) Usando a mão, calcule \( \cos(30^\circ) \).
👀 Ver solução passo a passo
30° → acima = 3.
$$\cos(30^\circ)=\frac{\sqrt{3}}{2}$$
Questão 3 — Tangente de 45°
(Médio) A partir da mão, encontre \( \tan(45^\circ) \).
👀 Ver solução passo a passo
45° → abaixo = 2, acima = 2.
$$\tan(45^\circ)=\sqrt{\frac{2}{2}}=1$$
Questão 4 — Aplicação com sombra
(Contexto real) Um poste projeta sombra de 4 m quando a elevação do Sol é 30°. Encontre a altura do poste.
👀 Ver solução passo a passo
Em triângulo retângulo: \(\tan(30^\circ)=\frac{\text{altura}}{\text{base}}\).
$$\tan(30^\circ)=\frac{\sqrt{3}}{3}$$
$$\frac{\sqrt{3}}{3}=\frac{h}{4}$$
$$h=\frac{4\sqrt{3}}{3}\ \text{m}$$
Questão 5 — Seno por complementaridade
(Relação) Mostre que \( \sin(30^\circ)=\cos(60^\circ) \) usando a mão.
👀 Ver solução passo a passo
30°: abaixo = 1 → \(\sin(30^\circ)=\frac{1}{2}\).
60°: acima = 1 → \(\cos(60^\circ)=\frac{1}{2}\).
Valores coincidem. Logo, \(\sin(30^\circ)=\cos(60^\circ)\).
Questão 6 — Tangente e razão entre dedos
(Raciocínio) Usando a tabela de dedos, calcule \( \tan(30^\circ) \).
👀 Ver solução passo a passo
30° → abaixo = 1, acima = 3.
$$\tan(30^\circ)=\sqrt{\frac{1}{3}}=\frac{\sqrt{3}}{3}$$
Conclusão
O método da mão é uma estratégia poderosa para estudantes de todos os níveis. Ele transforma a memorização de fórmulas em algo visual e fácil de aplicar. Agora você também tem um atalho confiável para a tangente. Sempre que precisar relembrar valores, consulte sua própria mão!
FAQ — Dúvidas Frequentes
Como saber qual dedo representa cada ângulo?
Comece com o polegar (0°) e siga até o mindinho (90°). Cada dedo centraliza um ângulo especial (30°, 45°, 60°). Dobre o dedo do ângulo desejado.
Esse método funciona para tangente?
Sim. Use \( \tan(\phi)=\sqrt{\frac{\text{abaixo}}{\text{acima}}} \). Basta contar os dedos após dobrar o dedo do ângulo.
Por que aparece a raiz e a divisão por 2?
A raiz vem da geometria dos ângulos notáveis; a divisão por 2 normaliza os valores de seno/cosseno no círculo trigonométrico unitário.
Posso usar em provas e concursos?
É ótimo para revisar mentalmente sem tabelas. Verifique apenas as regras da banca; o método é mnemônico, não exige aparelhos.
Autor: Adriano Rocha — Professor de Matemática, especialista em ensino prático e memorização.