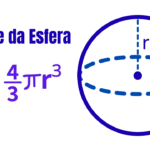
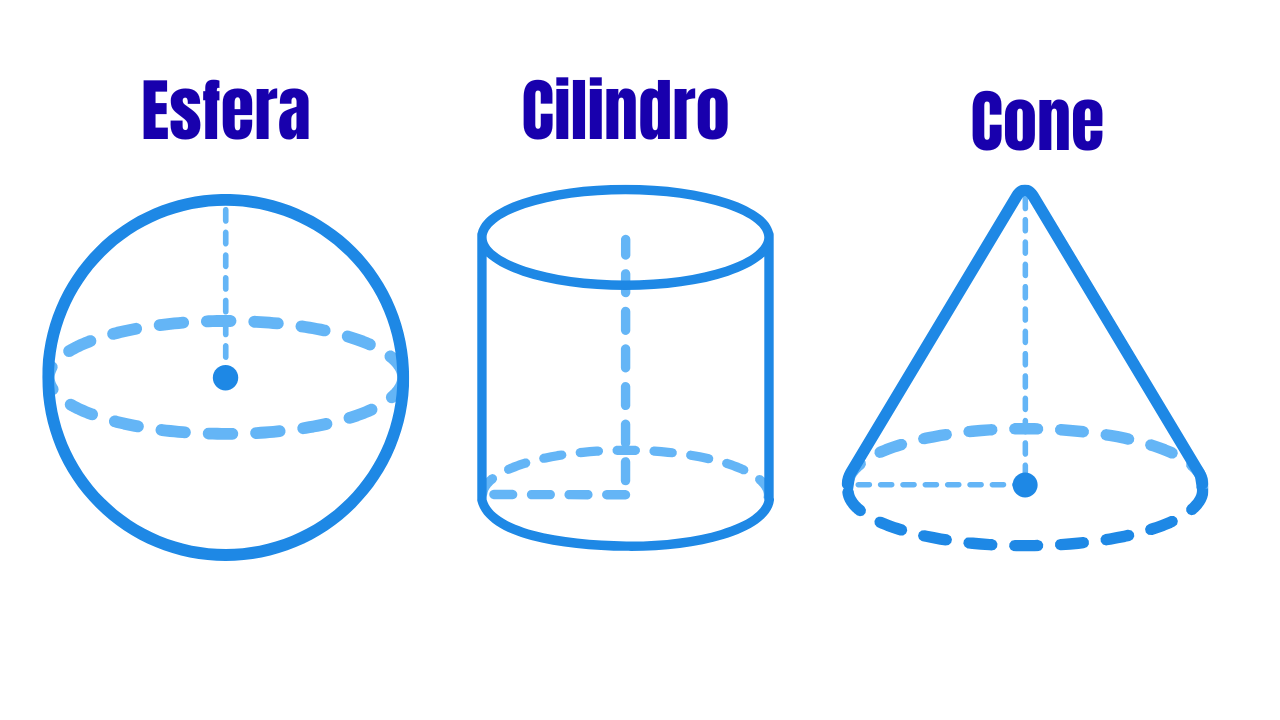
Corpos redondos: Esfera, Cilindro e Cone
Chamamos de corpos redondos os sólidos de revolução obtidos ao girar uma figura plana em torno de um eixo: a esfera surge do giro de um círculo em torno de um diâmetro; o cilindro, do giro de um retângulo em torno de um dos lados; e o cone, do giro de um triângulo retângulo em torno de um cateto. Eles aparecem em latas, reservatórios, bolas, copos e funis, além de inúmeras aplicações de engenharia.
Navegue neste artigo: Esfera • Cilindro • Cone • Exercícios
Convenções: \(r\) = raio, \(d=2r\) = diâmetro, \(h\) = altura, \(g\) = geratriz (cone), \(\pi\approx3{,}1416\).
Conteúdos relacionados no blog
- Sólidos de Platão — compare com os poliedros regulares.
- Dodecaedro • Octaedro • Icosaedro — reforço de geometria espacial.
- Tronco de Pirâmide • Razões de semelhança
Esfera
Conjunto dos pontos do espaço a distância fixa \(r\) (raio) de um centro. A “casca” é a superfície esférica; o sólido preenchido é a esfera cheia.
Área: \(\displaystyle A=4\pi r^2\).
Volume: \(\displaystyle V=\frac{4}{3}\pi r^3\).
Seção máxima (equador): \(\pi r^2\).
Escala: \(r\to k r \Rightarrow A\to k^2A, \; V\to k^3V\).
Observação útil: calotas esféricas (tampas) aparecem em caixas d’água e capacetes: área \(=2\pi R h\) e volume \(=\dfrac{\pi h^2(3R-h)}{3}\), onde \(R\) é o raio da esfera e \(h\) a altura da calota.
Cilindro reto
Possui duas bases circulares paralelas de raio \(r\) e altura \(h\). A superfície lateral, ao planificar, vira um retângulo de dimensões \(2\pi r \times h\).
Área lateral: \(\displaystyle A_L=2\pi r h\).
Área total: \(\displaystyle A_T=2\pi r h + 2\pi r^2 = 2\pi r(h+r)\).
Volume: \(\displaystyle V=\pi r^2 h\).
Conversão: 1 L = 1000 cm³.
Cone reto
Tem base circular de raio \(r\), altura \(h\) (perpendicular à base) e geratriz \(g\), que é a distância do vértice a um ponto da borda: \(g=\sqrt{r^2+h^2}\).
Área lateral: \(\displaystyle A_L=\pi r g\) (setor circular na planificação).
Área total: \(\displaystyle A_T=\pi r(g+r)\).
Volume: \(\displaystyle V=\dfrac{1}{3}\pi r^2 h\).
\(g=\sqrt{(R-r)^2+h^2}\), \(A_L=\pi(R+r)g\), \(V=\dfrac{\pi h}{3}\,(R^2+Rr+r^2)\).
Erros comuns (e como evitar)
- Área lateral ≠ total: em cilindros/cones, some as bases para a área total quando forem expostas.
- Usar \(g\) no volume do cone: o volume depende de \(h\), não da geratriz.
- Etiqueta do cilindro: a área do rótulo é apenas \(2\pi r h\).
- Unidades: verifique m²↔cm² (1 m² = 10 000 cm²) e L↔cm³ (1 L = 1000 cm³).
Materiais e produtos do blog
- Mapas Mentais de Matemática — revise fórmulas de área/volume rapidamente.
- ENEM Matemática — lista por competência com foco em geometria espacial.
- Pacote com 10 e-books — teoria + exercícios comentados.
- Banco de Questões de Matemática — centenas de itens por tema e dificuldade.
- Canais Oficiais de Matemática — acompanhe novidades e aulões.
Exercícios com situações-problema
Enunciados detalhados; soluções ocultas no sistema abre/fecha.
1) Reservatório cilíndrico
Um reservatório de água tem formato de cilindro reto com raio interno \(r=1{,}20\) m e altura \(h=3{,}00\) m. (a) Determine o volume em m³ e em litros. (b) Se for pintar a parte externa incluindo as duas tampas, qual é a área total a ser coberta?
Mostrar solução
\(V=\pi r^2h=\pi(1{,}2)^2\cdot3\approx13{,}57\ \text{m}^3=13\,570\ \text{L}\).
\(A_T=2\pi r(h+r)=2\pi\cdot1{,}2(3+1{,}2)=2\pi\cdot1{,}2\cdot4{,}2\approx31{,}58\ \text{m}^2\).
2) Rótulo de lata
Uma lata tem raio \(r=3{,}0\) cm e altura \(h=10{,}0\) cm. Qual é a área do rótulo (apenas a superfície lateral, sem tampas)?
Mostrar solução
\(A_L=2\pi r h=2\pi\cdot3\cdot10=60\pi\approx188{,}50\ \text{cm}^2\).
3) Copo cônico
Um copo tem formato de tronco de cone com raio superior \(R=4{,}0\) cm, raio inferior \(r=2{,}5\) cm e altura \(h=12{,}0\) cm. Encontre o volume em mililitros.
Mostrar solução
\(V=\frac{\pi h}{3}(R^2+Rr+r^2)=\frac{\pi\cdot12}{3}(16+10+6{,}25)\approx397{,}6\ \text{cm}^3\approx\mathbf{398\ \text{mL}}\).
4) Funil
Um funil é um cone reto com raio \(r=6\) cm e geratriz \(g=10\) cm. Determine a altura, a área lateral e a área total.
Mostrar solução
\(h=\sqrt{g^2-r^2}=\sqrt{100-36}=8\ \text{cm}\). \(A_L=\pi r g=\pi\cdot6\cdot10=60\pi\). \(A_T=A_L+\pi r^2=60\pi+36\pi=96\pi\ \text{cm}^2\).
5) Bola de treino
Uma bola esférica tem diâmetro \(d=6{,}7\) cm. Calcule a área da superfície e o volume da bola.
Mostrar solução
\(r=3{,}35\). Área \(A=4\pi r^2=4\pi\cdot(3{,}35)^2\approx141{,}0\ \text{cm}^2\). Volume \(V=\frac{4}{3}\pi r^3\approx157{,}3\ \text{cm}^3\).
6) Calota de caixa d’água
Em uma esfera de raio \(R=12\) cm recorta-se uma calota esférica de altura \(h=3\) cm (tampa). Encontre a área da tampa e o volume correspondente.
Mostrar solução
Área \(=2\pi R h=2\pi\cdot12\cdot3=72\pi\approx226{,}2\ \text{cm}^2\). Volume \(=\dfrac{\pi h^2(3R-h)}{3}=\dfrac{\pi\cdot9(36-3)}{3}=99\pi\approx311{,}0\ \text{cm}^3\).
7) Pintura de tubo
Um tubo cilíndrico de raio externo \(r=8\) cm e altura \(h=25\) cm será pintado apenas na área lateral externa a R$ 0,06 por cm². Qual o custo aproximado?
Mostrar solução
\(A_L=2\pi r h=2\pi\cdot8\cdot25=400\pi\approx1\,256{,}6\ \text{cm}^2\). Custo \(\approx0{,}06\cdot1\,256{,}6\approx\mathbf{R\$ 75{,}40}\).
8) Rolha de cortiça
Uma rolha é um cone maciço com \(r=1{,}5\) cm e \(h=4\) cm. Sabendo que a densidade da cortiça é \(0{,}65\ \text{g/cm}^3\), determine a massa da rolha.
Mostrar solução
Volume \(V=\frac{1}{3}\pi r^2 h=\frac{1}{3}\pi\cdot(1{,}5)^2\cdot4=3\pi\approx9{,}42\ \text{cm}^3\). Massa \(\approx0{,}65\cdot9{,}42=\mathbf{6{,}12\ \text{g}}\).
9) Escalonamento da esfera
O raio de uma esfera aumenta em 20% por re-projeto. Em que fator aumentam a área e o volume?
Mostrar solução
Fator linear \(k=1{,}20\). Área \(\times k^2=1{,}44\) (↑44%). Volume \(\times k^3=1{,}728\) (↑72,8%).
10) Lata com mesmo volume, menor rótulo
Duas latas têm mesmo volume \(V\): A com \((r,h)=(4\text{ cm},10\text{ cm})\) e B com \((r,h)=(5\text{ cm},6{,}4\text{ cm})\). Qual tem menor área de rótulo (área lateral)? Justifique pelos cálculos.
Mostrar solução
Como \(V=\pi r^2h\), ambas têm \(160\pi\ \text{cm}^3\). Áreas laterais: A → \(2\pi rh=80\pi\), B → \(2\pi\cdot5\cdot6{,}4=64\pi\). Logo a lata B usa menos área de rótulo.
Quer continuar estudando?
Explore os sólidos geométricos no blog e amplie seus exercícios com nossos materiais: