Demonstração da Fórmula de Bhaskara
A Fórmula de Bhaskara resolve qualquer equação do 2º grau \(ax^2+bx+c=0\) (com \(a\neq 0\)). A seguir, mostramos a demonstração completar quadrados, o porquê do discriminante \(\Delta\) e exemplos em coluna.
Resultado final
\[
x=\frac{-b\pm\sqrt{b^2-4ac}}{2a},\qquad \Delta=b^2-4ac.
\]
Pré-requisitos
- \(a\neq 0\) (senão é 1º grau).
- Propriedade: \(u^2+2uv+v^2=(u+v)^2\).

Prova por completar quadrados (passo a passo)
\[
\begin{aligned}
&ax^2+bx+c=0 \qquad (a\neq 0)\\[4pt]
&\text{Dividindo por }a:\\
&x^2+\frac{b}{a}x+\frac{c}{a}=0\\[4pt]
&\text{Isolando os termos em }x:\\
&x^2+\frac{b}{a}x=-\frac{c}{a}\\[4pt]
&\text{Somando } \left(\frac{b}{2a}\right)^2 \text{ aos dois lados:}\\
&x^2+\frac{b}{a}x+\left(\frac{b}{2a}\right)^2
=-\frac{c}{a}+\left(\frac{b}{2a}\right)^2\\[4pt]
&\text{Trinômio quadrado perfeito:}\\
&\left(x+\frac{b}{2a}\right)^2
=-\frac{c}{a}+\frac{b^2}{4a^2}\\[4pt]
&\text{Colocando em denominador comum }4a^2:\\
&\left(x+\frac{b}{2a}\right)^2
=\frac{b^2-4ac}{4a^2}\\[6pt]
&\text{Extraindo a raiz (±):}\\
&x+\frac{b}{2a}=\pm\frac{\sqrt{b^2-4ac}}{2a}\\[6pt]
&\text{Isolando }x:\\
&x=-\frac{b}{2a}\pm\frac{\sqrt{b^2-4ac}}{2a}\\[2pt]
&x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}.
\end{aligned}
\]
O papel do discriminante \(\Delta\)
- \(\Delta=b^2-4ac\).
- \(\Delta>0\): duas raízes reais distintas.
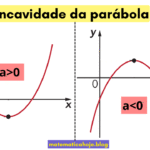
- \(\Delta=0\): uma raiz real dupla (a parábola toca o eixo \(x\)).
- \(\Delta<0\): sem raízes reais (raízes complexas conjugadas).
📘 E-book de Fórmulas de Matemática
Tenha Bhaskara, forma canônica, vértice, produtos notáveis e muito mais em um só lugar para revisões rápidas.
Quero o E-book de FórmulasExemplos resolvidos (contas uma embaixo da outra)
Exemplo 1 — \(x^2-5x+6=0\)
\[
\begin{aligned}
a&=1,\ b=-5,\ c=6\\[2pt]
\Delta&=b^2-4ac\\
&=(-5)^2-4(1)(6)\\
&=25-24\\
&=1\\[6pt]
x&=\frac{-b\pm\sqrt{\Delta}}{2a}\\
&=\frac{-(-5)\pm\sqrt{1}}{2\cdot 1}\\
&=\frac{5\pm 1}{2}\\[6pt]
x_1&=\frac{6}{2}=3,\qquad x_2=\frac{4}{2}=2
\end{aligned}
\]
Exemplo 2 — \(2x^2+3x-2=0\)
\[
\begin{aligned}
a&=2,\ b=3,\ c=-2\\[2pt]
\Delta&=3^2-4(2)(-2)\\
&=9+16\\
&=25\\[6pt]
x&=\frac{-3\pm\sqrt{25}}{2\cdot 2}\\
&=\frac{-3\pm 5}{4}\\[6pt]
x_1&=\frac{2}{4}=\frac{1}{2},\qquad
x_2=\frac{-8}{4}=-2
\end{aligned}
\]
Erros comuns
- Esquecer o “\(\pm\)” ao extrair a raiz.
- Trocar sinais de \(b\) ou de \(\sqrt{\Delta}\).
- Usar a fórmula com \(a=0\) (nesse caso é 1º grau).
Exercícios propostos
1) Resolva \(x^2-4x+1=0\) por Bhaskara.
Gabarito
\[
\begin{aligned}
a&=1,\ b=-4,\ c=1\\
\Delta&=(-4)^2-4(1)(1)=16-4=12\\
x&=\frac{-(-4)\pm\sqrt{12}}{2}\\
&=\frac{4\pm 2\sqrt{3}}{2}\\
&=2\pm\sqrt{3}
\end{aligned}
\]
2) Calcule as raízes de \(3x^2-6x+3=0\).
Gabarito
\[
\begin{aligned}
a&=3,\ b=-6,\ c=3\\
\Delta&=(-6)^2-4(3)(3)=36-36=0\\
x&=\frac{-(-6)\pm 0}{2\cdot 3}=\frac{6}{6}=1
\end{aligned}
\]
Raiz dupla \(x=1\).
3) Mostre que \(x^2+2x+5=0\) não tem raízes reais.
Gabarito
\[
\begin{aligned}
a&=1,\ b=2,\ c=5\\
\Delta&=2^2-4(1)(5)=4-20=-16<0
\end{aligned}
\]
Logo, as raízes são complexas.
Continue estudando (links internos)
Função Quadrática (guia completo)
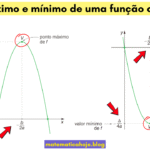
Valor máximo e mínimo
Gráfico da função quadrática
Vértice da parábola
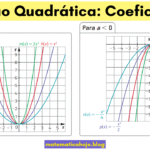
Coeficiente \(a\)
Coeficientes \(b\) e \(c\)
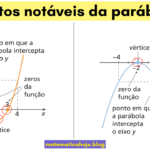
Pontos notáveis da parábola