Nesta questão de Geometria Plana do ENEM 2025, analisamos dois projetos de túnel, ambos em forma de semicilindro reto (com seção transversal semicircular), para decidir qual deles remove menor quantidade de material da montanha. O critério de escolha é a menor área de seção transversal.
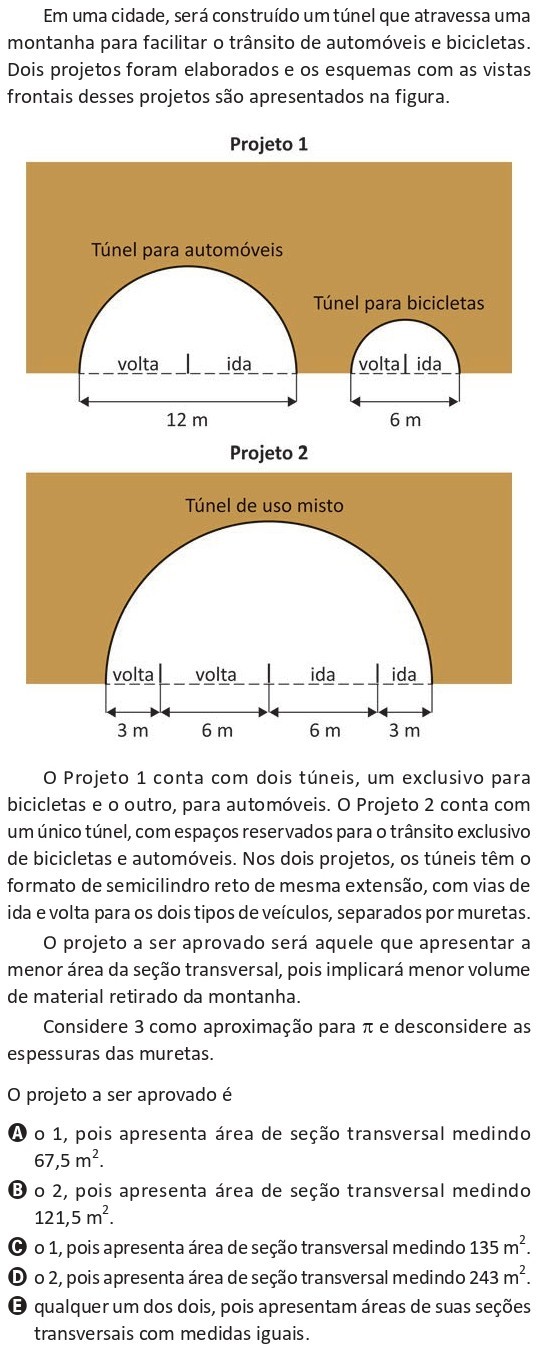
O Projeto 1 possui dois túneis semicirculares: um para automóveis, com 12 m de largura, e outro para bicicletas, com 6 m de largura. O Projeto 2 possui um único túnel semicircular, usado de forma mista, com 18 m de largura. Adota-se π ≈ 3 e desconsideram-se as espessuras das muretas.
✅ Ver solução passo a passo
1) Fórmula da área de um semicírculo
A área de um círculo de raio r é A = π·r². Como os túneis são semicírculos, a área da seção transversal é:
Asemicírculo = (π·r²) / 2
Vamos usar π ≈ 3, como pede o enunciado.
2) Área total do Projeto 1
Túnel para automóveis
- Diâmetro = 12 m ⇒ raio r = 12 / 2 = 6 m.
- Área: Acarros = (π·6²) / 2 = (3·36) / 2 = 108 / 2 = 54 m².
Túnel para bicicletas
- Diâmetro = 6 m ⇒ raio r = 6 / 2 = 3 m.
- Área: Abikes = (π·3²) / 2 = (3·9) / 2 = 27 / 2 = 13,5 m².
Área total do Projeto 1:
A1 = 54 + 13,5 = 67,5 m².
3) Área do Projeto 2
No Projeto 2 há apenas um túnel semicircular, com largura total 3 + 6 + 6 + 3 = 18 m.
- Diâmetro = 18 m ⇒ raio r = 18 / 2 = 9 m.
- Área: A2 = (π·9²) / 2 = (3·81) / 2 = 243 / 2 = 121,5 m².
4) Comparando as áreas
Projeto 1: A1 = 67,5 m² Projeto 2: A2 = 121,5 m²
Como o projeto a ser aprovado deve apresentar a menor área de seção transversal, a escolha recai sobre o Projeto 1.
✅ Projeto aprovado: Projeto 1, com área de 67,5 m².
✅ Alternativa correta: A
Questão anterior resolvida: ENEM 2025 – Logaritmos: pressão em máquinas e escolha do parâmetro K
📚 Continue estudando para o ENEM com o Matemática Hoje:

























