Função Exponencial — leitura de gráfico e transformações
Uma abordagem visual e prática: como reconhecer e montar \(f(x)=A\cdot B^{(x-x_0)}+C\) a partir do gráfico.
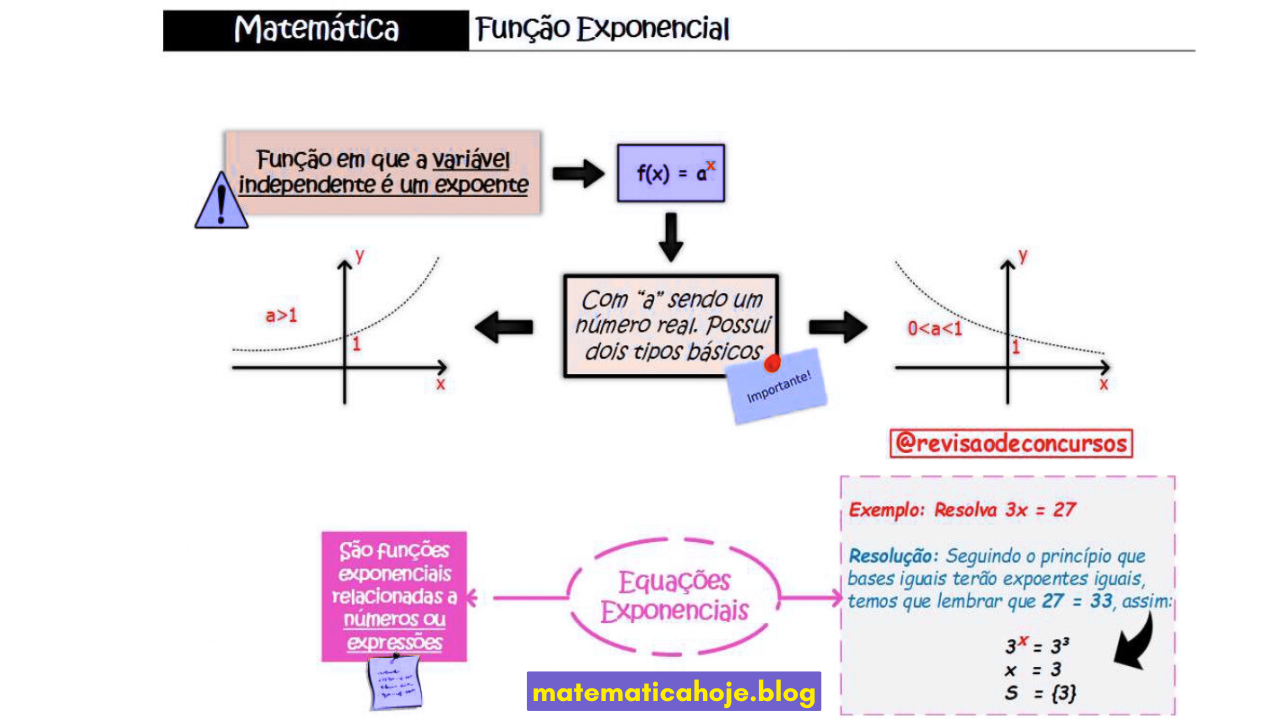
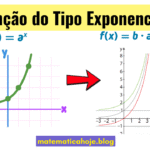
Ideia central. Chamaremos de função exponencial qualquer função do tipo
\[ f(x)=A\cdot B^{(x-x_0)}+C, \qquad B>0,\; B\ne1. \]
Esse formato generaliza \(a^x\) e facilita a leitura do gráfico:
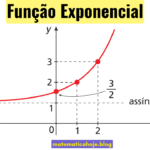
- C é a assíntota horizontal (altura onde o gráfico “encosta” ao ir para \(-\infty\)).
- A estica/inverte o gráfico. Se \(A>0\) fica acima da assíntota; se \(A<0\) reflete.
- x₀ desloca o gráfico para a direita/esquerda.
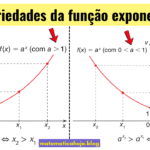
- B define o comportamento: B>1 → crescente 0<B<1 → decrescente.
1) Como “ler” uma exponencial em 4 passos
- Localize a assíntota horizontal ⇒ valor de \(C\).
- Use o ponto âncora \(x=x_0\): como \(B^{(x_0-x_0)}=1\), então \(f(x_0)=A+C\).
- Leia um segundo ponto para descobrir \(B\): \(\displaystyle \frac{f(x_0+\Delta x)-C}{A}=B^{\Delta x}\Rightarrow B=\left(\frac{f(x_0+\Delta x)-C}{A}\right)^{1/\Delta x}\).
- Verifique a monotonicidade (crescente/decrescente) e ajuste o sinal de \(A\) se necessário.
📘 Tenha fórmulas e “macetes” de funções (exponencial, log, quadrática, progressões) num só material:
Baixe o eBook Fórmulas Matemática
Baixe o eBook Fórmulas Matemática
2) Duas famílias no mesmo olhar
Crescente (\(B>1\))
Aproxima-se da assíntota quando \(x\to-\infty\) e dispara para \(+\infty\) quando \(x\to+\infty\). Ex.: \(f(x)=2\cdot 3^{x-1}+1\) ⇒ assíntota \(y=1\), ponto âncora \((1,3)\).
Aproxima-se da assíntota quando \(x\to-\infty\) e dispara para \(+\infty\) quando \(x\to+\infty\). Ex.: \(f(x)=2\cdot 3^{x-1}+1\) ⇒ assíntota \(y=1\), ponto âncora \((1,3)\).
Decrescente (\(0<B<1\))
Aproxima-se da assíntota quando \(x\to+\infty\). Ex.: \(g(x)=5\cdot (1/2)^{x+2}-3\) ⇒ assíntota \(y=-3\), ponto âncora \((-2,2)\).
Aproxima-se da assíntota quando \(x\to+\infty\). Ex.: \(g(x)=5\cdot (1/2)^{x+2}-3\) ⇒ assíntota \(y=-3\), ponto âncora \((-2,2)\).
3) Por que \(a^x\) aparece tanto?
Qualquer exponencial pode ser vista como \(A\cdot e^{k(x-x_0)}+C\) porque \(B^{x}=e^{x\ln B}\). Isso permite ler taxas contínuas \(k=\ln B\) (útil em crescimento exponencial e decaimento).4) Equações exponenciais sem sofrimento
Três estratégias que cobrem 90% dos exercícios:
- Comparação de bases: transforme tudo na mesma base. Ex.: \(3^{x}=27 \Rightarrow 3^{x}=3^{3} \Rightarrow x=3\).
- Isolar a exponencial e aplicar logaritmo: \(5^{2x-1}=40 \Rightarrow (2x-1)\ln5=\ln40 \Rightarrow x=\dfrac{\ln40+\ln5}{2\ln5}\).
- Usar o ponto âncora da forma \(A\cdot B^{(x-x_0)}+C\) quando o gráfico/assíntota é dado.
5) Exemplos resolvidos
Exemplo 1 — Reconstruindo a lei a partir do gráfico. A assíntota é \(y=1\). O gráfico passa por \((1,3)\) e \((2,6)\). Encontre \(f(x)\) na forma \(A\cdot B^{(x-x_0)}+C\).
Da assíntota: \(C=1\). Tome \(x_0=1\) (ponto âncora). Então \(f(1)=A+C=3\Rightarrow A=2\).
Use \((2,6)\): \(6=2\cdot B^{(2-1)}+1\Rightarrow 5=2B\Rightarrow B=\tfrac{5}{2}\).
Logo: \(\displaystyle f(x)=2\left(\tfrac{5}{2}\right)^{(x-1)}+1\).
Exemplo 2 — Tempo de duplicação. Uma população segue \(P(t)=P_0\cdot B^t\). Se cresce 8% ao período, ache o tempo de duplicação.
\(B=1{,}08\). Duplicação: \(2=P(t)/P_0=B^t\Rightarrow t=\dfrac{\ln2}{\ln1{,}08}\approx 9{,}01\) períodos.
Exemplo 3 — Equação exponencial. Resolva \(2^{x+1}+2^{x}=96\).
Fatora exponenciais: \(2^{x}(2+1)=3\cdot 2^{x}=96\Rightarrow 2^{x}=32\Rightarrow x=5\).
📘 Reforce agora: fórmulas, curvas-padrão e “macetes” de funções.
Baixe o eBook Fórmulas Matemática
Baixe o eBook Fórmulas Matemática
6) Checklist rápido (para provas)
- Assíntota \(y=C\) identificada?
- O ponto âncora \((x_0,A+C)\) aparece no gráfico/tabela?
- \(B>1\) (cresce) ou \(0<B<1\) (decresce)?
- Reescreveu como \(e^{kx}\) se precisar de taxa contínua?
7) Exercícios propostos
- Monte a função com assíntota \(y=-2\), ponto âncora \((0,1)\) e \(B=3\).
- Resolva \(5^{x-2}=4\cdot 5^{-x}\).
- Uma substância decai 12% por hora. Escreva \(Q(t)\) e calcule o tempo de meia-vida.
📚 Materiais recomendados do blog
🧠 Mapas Mentais de Matemática 🎯 ENEM Matemática 📚 Coleção 10 eBooks 📝 Banco de Questões de Matemática 📘 eBook Fórmulas MatemáticaLeituras internas relacionadas: Crescimento exponencial • Notação científica • Potenciação