Função Exponencial: Crescente ou Decrescente – Questão Resolvida

🔎 Entendendo o enunciado:

Devemos classificar as funções exponenciais como crescente ou decrescente. Para isso, devemos analisar a base da potência e o sinal do expoente.

1) Lembrete teórico:

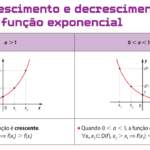
Uma função exponencial \( f(x) = a^x \):
– É crescente se \( a > 1 \)
– É decrescente se \( 0 < a < 1 \)
– Se a base é invertida por um expoente negativo, também resulta em função decrescente.

2) Analisando cada item:

• a) \( f(x) = 5^x \) → base \( > 1 \) → crescente
• b) \( f(x) = \left(\frac{1}{6}\right)^x \) → base \( < 1 \) → decrescente
• c) \( f(x) = 2^{-x} \) → \( 2^{-x} = \left(\frac{1}{2}\right)^x \) → base \( < 1 \) → decrescente
• d) \( f(x) = 3^{x/2} \) → base \( > 1 \), e expoente linear positivo → crescente

✅ Conclusão:

• a) Crescente
• b) Decrescente
• c) Decrescente
• d) Crescente