Função Quadrática: Coeficientes b e c

Função Quadrática: o que os coeficientes <em>b</em> e <em>c</em> fazem?

Função Quadrática: como b e c mexem no gráfico?

Na forma \(f(x)=ax^2+bx+c\) (\(a\neq0\)), já vimos que \(a\) controla a concavidade e a abertura. Mas quem posiciona horizontal e verticalmente a parábola são os coeficientes \(b\) e \(c\). Abaixo estão as ideias-chave e exemplos rápidos.

1) Resumo visual do papel de b e c

Coeficiente b — deslocamento horizontal

Define a posição do eixo de simetria: \(x_v=-\dfrac{b}{2a}\).
Com \(a\) e \(c\) fixos, trocar \(b\to -b\) produz um espelhamento no eixo \(y\): \(a x^2 + b x + c \mapsto a x^2 – b x + c = f(-x)\).
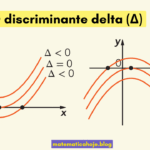
Influencia os zeros e o vértice (pois entra em \(\Delta=b^2-4ac\) e em \(x_v\)).

Coeficiente c — translação vertical

É sempre o intercepto em \(y\): \(f(0)=c\Rightarrow (0,c)\).
Com \(a\) e \(b\) fixos, variar \(c\) move a parábola para cima/baixo sem mudar o eixo \(x=x_v\).
Também altera \(\Delta=b^2-4ac\) e pode criar/eliminar raízes reais.

Ligação com a forma canônica

Completando quadrado: \[ ax^2+bx+c=a\Bigl(x+\frac{b}{2a}\Bigr)^2+\Bigl(c-\frac{b^2}{4a}\Bigr). \] O vértice é \( \bigl(-\tfrac{b}{2a},\, c-\tfrac{b^2}{4a}\bigr)\).

Comparação do efeito dos coeficientes b e c em y=x²+bx+c: troca do sinal de b gera espelhamento e c define o ponto em que o gráfico corta o eixo y.

2) Exemplos resolvidos (contas uma embaixo da outra)

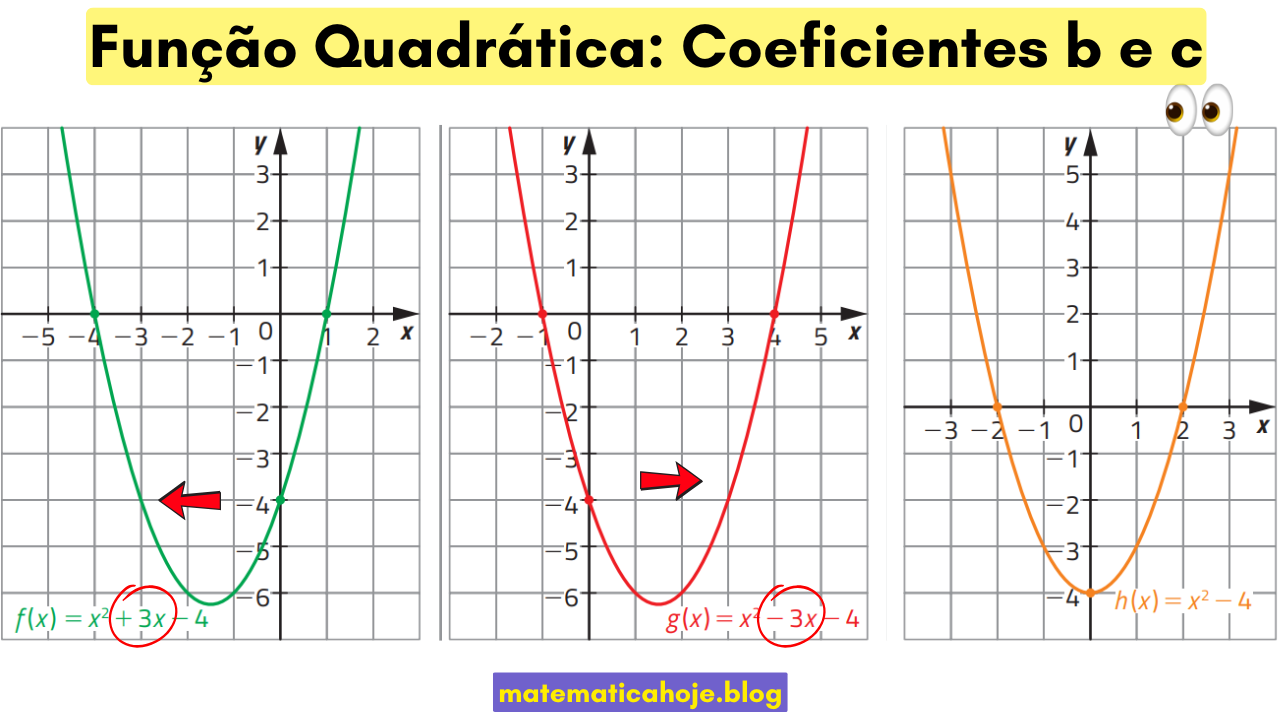
Exemplo A — Espelhamento ao trocar o sinal de b

Compare \(f(x)=x^2+3x-4\) e \(g(x)=x^2-3x-4\). Mostre que os gráficos são simétricos em relação ao eixo \(y\) e calcule os notáveis.

\[ \begin{aligned} \text{Para } f(x):\ a&=1,\ b=3,\ c=-4\\[2pt] x_v&=-\frac{b}{2a}\\ &=-\frac{3}{2}\\ &= -1{,}5\\[4pt] \Delta&=b^2-4ac\\ &= 9 – 4(1)(-4)\\ &= 9 + 16\\ &= 25\\[4pt] x_{1,2}&=\frac{-b\pm\sqrt{\Delta}}{2a}\\ &=\frac{-3\pm 5}{2}\\ &=\{-4,\ 1\}\\[8pt] \text{Para } g(x):\ a&=1,\ b=-3,\ c=-4\\[2pt] x_v&=-\frac{-3}{2}\\ &=\frac{3}{2}\\ &= 1{,}5\\[4pt] \Delta&=(-3)^2-4(1)(-4)\\ &= 9 + 16\\ &= 25\\[4pt] x_{1,2}&=\frac{3\pm 5}{2}\\ &=\{-1,\ 4\} \end{aligned} \]

Note que os pares de raízes \(\{-4,1\}\) e \(\{-1,4\}\) são imagens por reflexão em \(x=0\), e os eixos \(x=\pm 1{,}5\) também.

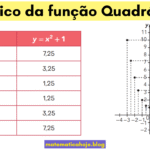
Exemplo B — Variar apenas c desloca o gráfico para cima/baixo

Compare \(p(x)=x^2+3x-4\) (de cima) com \(q(x)=x^2+3x+2\) (mesmos \(a\) e \(b\), mas \(c\) diferente).

\[ \begin{aligned} \text{Eixo (ambas)}:\ x_v&=-\frac{3}{2}=-1{,}5\\[6pt] \text{Para } p:\ \Delta_p&=3^2-4(1)(-4)=25\\ x_{1,2}&=\frac{-3\pm 5}{2}=\{-4,\ 1\}\\ p(0)&=c=-4\\[8pt] \text{Para } q:\ \Delta_q&=3^2-4(1)(2)=1\\ x_{1,2}&=\frac{-3\pm 1}{2}=\{-2,\ -1\}\\ q(0)&=c=2 \end{aligned} \]

Mudou apenas \(c\) e toda a parábola subiu \(6\) unidades (de \(-4\) para \(2\)), preservando o mesmo eixo \(x=-1{,}5\).

Exemplo C — Encontre \(b\) e \(c\) por condições

Suponha \(f(x)=x^2+bx+c\) passa por \((0,-4)\) e tem vértice em \(x=1{,}5\). Determine \(b\) e \(c\).

\[ \begin{aligned} f(0)&=c\\ &=-4\\ \Rightarrow c&=-4\\[6pt] x_v&=-\frac{b}{2a}\\ &=-\frac{b}{2\cdot 1}\\ &=1{,}5\\ -\frac{b}{2}&=1{,}5\\ b&=-3 \end{aligned} \]

3) Erros comuns (e como evitar)

Confundir \(c\) com a ordenada do vértice. Não! \(c=f(0)\); a ordenada do vértice é \(y_v=-\dfrac{\Delta}{4a}\).
Achar que \(b\) “anda o gráfico” para a direita/esquerda como em \(y=(x-h)^2\). O que \(b\) faz é definir o eixo \(x_v=-\dfrac{b}{2a}\); o deslocamento horizontal fica explícito na forma canônica \(y=a(x-h)^2+k\).
Trocar \(b\) por \(-b\) não translada: reflete o gráfico no eixo \(y\) quando \(a\) e \(c\) são mantidos.

4) Exercícios propostos

1) Para \(f(x)=2x^2-6x+c\), determine \(c\) para que o intercepto em \(y\) seja \(4\) e encontre o vértice.

Gabarito

\[ \begin{aligned} f(0)&=c\\ &=4\\ x_v&=-\frac{b}{2a}=-\frac{-6}{4}=\frac{3}{2}\\ y_v&=f\!\left(\tfrac{3}{2}\right)=2\left(\tfrac{9}{4}\right)-6\left(\tfrac{3}{2}\right)+4\\ &=\tfrac{9}{2}-9+4\\ &=\tfrac{9}{2}-5\\ &= -\tfrac{1}{2} \end{aligned} \]

2) Mostre que \(f(x)=x^2+bx-4\) e \(g(x)=x^2-bx-4\) são simétricas em relação ao eixo \(y\).

Gabarito

Basta notar que \(g(x)=f(-x)\): \(f(-x)=(-x)^2+b(-x)-4=x^2-bx-4=g(x)\). Assim, os gráficos são espelhos em \(x=0\).

3) Em \(h(x)=x^2+3x+c\), qual \(c\) faz com que a parábola toque o eixo \(x\) (raiz dupla)?

Gabarito

\[ \begin{aligned} \Delta&=b^2-4ac\\ &=3^2-4(1)c\\ &=9-4c\\ \Delta&=0\\ 9-4c&=0\\ c&=\tfrac{9}{4} \end{aligned} \]

5) Para se aprofundar

Função Quadrática (guia completo) Coeficiente \(a\) no gráfico Pontos notáveis da parábola Como construir o gráfico A parábola (foco e diretriz) Sinal da função

Relacionadas

Gráfico da Função Quadrática

Função Quadrática

Forma fatorada da Função Quadrática

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.