Questão 49. (FGV-SP) A figura fornece os gráficos dos lucros anuais \( L_A \) e \( L_B \) de duas empresas (em milhares de reais) em função da quantidade anual produzida e vendida (\( x \)).
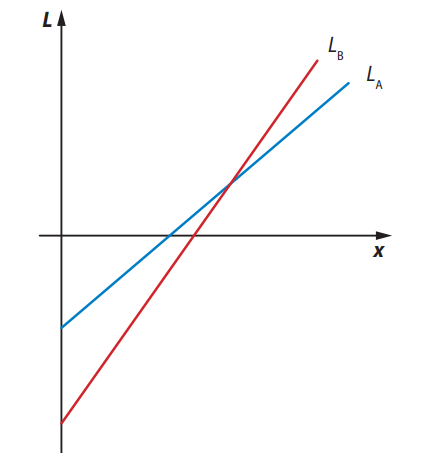
As interseções dos gráficos com os eixos são:
| Ponto | \( L_A \) | \( L_B \) |
|---|---|---|
| Eixo x | (50, 0) | (60, 0) |
| Eixo y | (0, -500) | (0, -1000) |
a) Obtenha \( L_A \) em função de \( x \).
b) Para que valores de \( x \) o lucro \( L_B \) é superior ao \( L_A \)?
🔍 Ver solução passo a passo
🔎 Entendendo o gráfico:
Temos duas funções afins do tipo \( L(x) = mx + b \), onde \( m \) é o coeficiente angular (taxa de variação) e \( b \) é o lucro inicial (intercepto em \( y \)).
1) Item a – Função \( L_A \):
Sabemos que passa pelos pontos (0, –500) e (50, 0).
Calculando o coeficiente angular:
$$ m = \frac{0 – (-500)}{50 – 0} = \frac{500}{50} = 10 $$
Logo, a função \( L_A(x) \) é:
$$ L_A(x) = 10x – 500 $$
2) Item b – Quando \( L_B > L_A \):
Função \( L_B \): passa por (0, –1000) e (60, 0)
Coeficiente angular:
$$ m = \frac{0 – (-1000)}{60 – 0} = \frac{1000}{60} = \frac{50}{3} $$
Então, \( L_B(x) = \frac{50}{3}x – 1000 \)
Queremos saber quando:
$$ L_B(x) > L_A(x) \Rightarrow \frac{50}{3}x – 1000 > 10x – 500 $$
Multiplicando tudo por 3 para eliminar denominador:
$$ 50x – 3000 > 30x – 1500 \Rightarrow 20x > 1500 \Rightarrow x > 75 $$
✅ Conclusão:
- a) \( L_A(x) = 10x – 500 \)
- b) \( L_B > L_A \) quando \( x > 75 \)




























