Funções Elementares
Constante, linear, valor absoluto, quadrática, cúbica, exponencial, raiz quadrada, raiz cúbica e recíproca — com propriedades e exercícios.
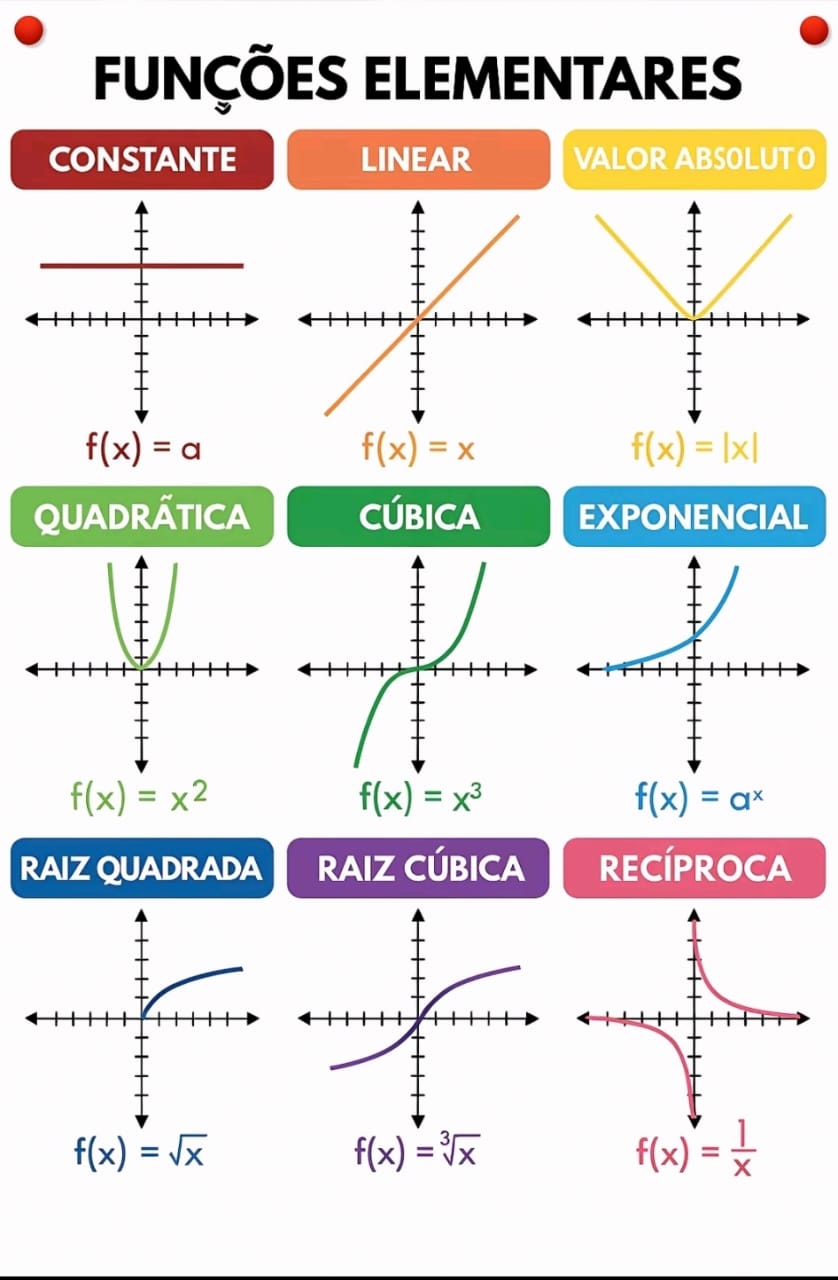
Panorama
Constante: \(f(x)=a\)
Linear: \(f(x)=mx+b\)
Valor absoluto: \(f(x)=|x|\)
Quadrática: \(f(x)=ax^2+bx+c\)
Cúbica: \(f(x)=ax^3+bx^2+cx+d\)
Exponencial: \(f(x)=a^x\) (\(a>0,a\neq1\))
Raiz quadrada: \(f(x)=\sqrt{x}\)
Raiz cúbica: \(f(x)=\sqrt[3]{x}\)
Recíproca: \(f(x)=\frac{1}{x}\)
Transformações úteis
Translações: \(f(x-k)+c\) move o gráfico \(k\) para a direita e \(c\) para cima.
Reflexões: \(f(-x)\) reflete no eixo \(y\); \(-f(x)\) reflete no eixo \(x\).
Escalas: \(af(x)\) estica verticalmente; \(f(bx)\) comprime/estica horizontalmente.
Reflexões: \(f(-x)\) reflete no eixo \(y\); \(-f(x)\) reflete no eixo \(x\).
Escalas: \(af(x)\) estica verticalmente; \(f(bx)\) comprime/estica horizontalmente.
Tabela-resumo
| Família | Domínio | Imagem | Paridade | Monotonia (típica) | Assíntotas |
|---|---|---|---|---|---|
| Constante \(a\) | \(\mathbb{R}\) | \(\{a\}\) | — | Constante | — |
| Linear \(mx+b\) | \(\mathbb{R}\) | \(\mathbb{R}\) | — | ↑ se \(m>0\), ↓ se \(m<0\) | — |
| |x| | \(\mathbb{R}\) | \([0,\infty)\) | par | ↓ em \((-\infty,0]\), ↑ em \([0,\infty)\) | — |
| Quadrática | \(\mathbb{R}\) | \([f_{\min},\infty)\) se \(a>0\); \((-\infty,f_{\max}]\) se \(a<0\) | — | ↧ até o vértice / ↥ após | — |
| Cúbica \(x^3\) (modelo) | \(\mathbb{R}\) | \(\mathbb{R}\) | ímpar | ↑ em todo \(\mathbb{R}\) | — |
| Exponencial \(a^x\) | \(\mathbb{R}\) | \((0,\infty)\) | — | ↑ se \(a>1\), ↓ se \(0| Horizontal: \(y=0\) | |
| \(\sqrt{x}\) | \([0,\infty)\) | \([0,\infty)\) | — | ↑ em \([0,\infty)\) | — |
| \(\sqrt[3]{x}\) | \(\mathbb{R}\) | \(\mathbb{R}\) | ímpar | ↑ em todo \(\mathbb{R}\) | — |
| Recíproca \(1/x\) | \(\mathbb{R}\setminus\{0\}\) | \(\mathbb{R}\setminus\{0\}\) | ímpar | ↓ em \((-\infty,0)\) e \((0,\infty)\) | Vert.: \(x=0\), Horiz.: \(y=0\) |
Exemplos rápidos
1) Vértice da quadrática \(f(x)=x^2-4x+7\): \(x_v=-\frac{b}{2a}=2\), \(f(2)=3\).
2) Exponencial \(g(x)=2^x\): \(g(0)=1\), assíntota horizontal \(y=0\).
3) Raiz quadrada \(h(x)=\sqrt{x-4}\): domínio \([4,\infty)\).
Exercícios (múltipla escolha)
1) O domínio de \(f(x)=\sqrt{x}\) é:
- \(\mathbb{R}\)
- \((-\infty,0]\)
- \([0,\infty)\)
- \((0,\infty)\)
Mostrar solução
Para raiz quadrada real, \(x\ge0\). Alternativa c.
2) Qual afirmação é verdadeira para \(g(x)=2^x\)?
- Domínio \((0,\infty)\)
- Imagem \((0,\infty)\)
- Assíntota vertical \(x=0\)
- \(g(0)=0\)
Mostrar solução
Exponencial tem domínio \(\mathbb{R}\) e imagem \((0,\infty)\). Alternativa correta: b.
3) O gráfico de \(f(x)=|x-2|+1\) tem vértice em:
- \((0,0)\)
- \((2,1)\)
- \((-2,1)\)
- \((1,2)\)
Mostrar solução
Translação do vértice para \((2,1)\). Alternativa b.
4) Para \(f(x)=mx+b\), se \(f(1)=3\) e \(f(3)=7\), então \(m\) e \(b\) valem:
- \(m=2,\ b=1\)
- \(m=1,\ b=2\)
- \(m=4,\ b=-1\)
- \(m=2,\ b=0\)
Mostrar solução
Inclinação \(m=(7-3)/(3-1)=2\). De \(3=2\cdot1+b\Rightarrow b=1\). Alternativa a.
5) A imagem de \(f(x)=\frac{1}{x}\) é:
- \(\mathbb{R}\)
- \(\mathbb{R}\setminus\{0\}\)
- \((0,\infty)\)
- \((-\infty,0)\)
Mostrar solução
Nunca zera. Imagem \(\mathbb{R}\setminus\{0\}\). Alternativa b.
6) Para \(p(x)=x^2-4x+7\), o valor mínimo é:
- \(-1\)
- \(3\)
- \(4\)
- \(7\)
Mostrar solução
Vértice em \(x=2\): \(p(2)=3\). Alternativa b.
7) Resolva \(q(x)=x^3-2x\) em \(x=-1\):
- \(-3\)
- \(1\)
- \(-1\)
- \(3\)
Mostrar solução
\((-1)^3-2(-1)=-1+2=1\). Alternativa b.
8) O domínio de \(r(x)=\sqrt{x-4}\) é:
- \((-\infty,4)\)
- \([4,\infty)\)
- \((4,\infty)\)
- \(\mathbb{R}\)
Mostrar solução
Exige \(x-4\ge0\Rightarrow x\ge4\). Alternativa b.
9) A função \(s(x)=\sqrt[3]{x}\) é:
- Par
- Ímpar
- Constante
- Periódica
Mostrar solução
\(s(-x)=-\sqrt[3]{x}\Rightarrow\) ímpar. Alternativa b.
10) A desigualdade \(\frac{1}{x}>0\) é satisfeita por:
- \(x>0\)
- \(x<0\)
- \(x\neq0\)
- \(x=0\)
Mostrar solução
\(1/x\) é positiva somente para \(x>0\). Alternativa a.
Leituras relacionadas
Aprofunde: quadrática e vértice, crescimento de exponenciais, propriedades do valor absoluto e assíntotas de funções racionais.





























