Funções inversas

Se \(f:A\to B\) é uma função, sua inversa \(f^{-1}:B\to A\) “desfaz” a ação de \(f\). Na prática, invertemos pares ordenados: \((x,y)\) em \(f\) vira \((y,x)\) em \(f^{-1}\).

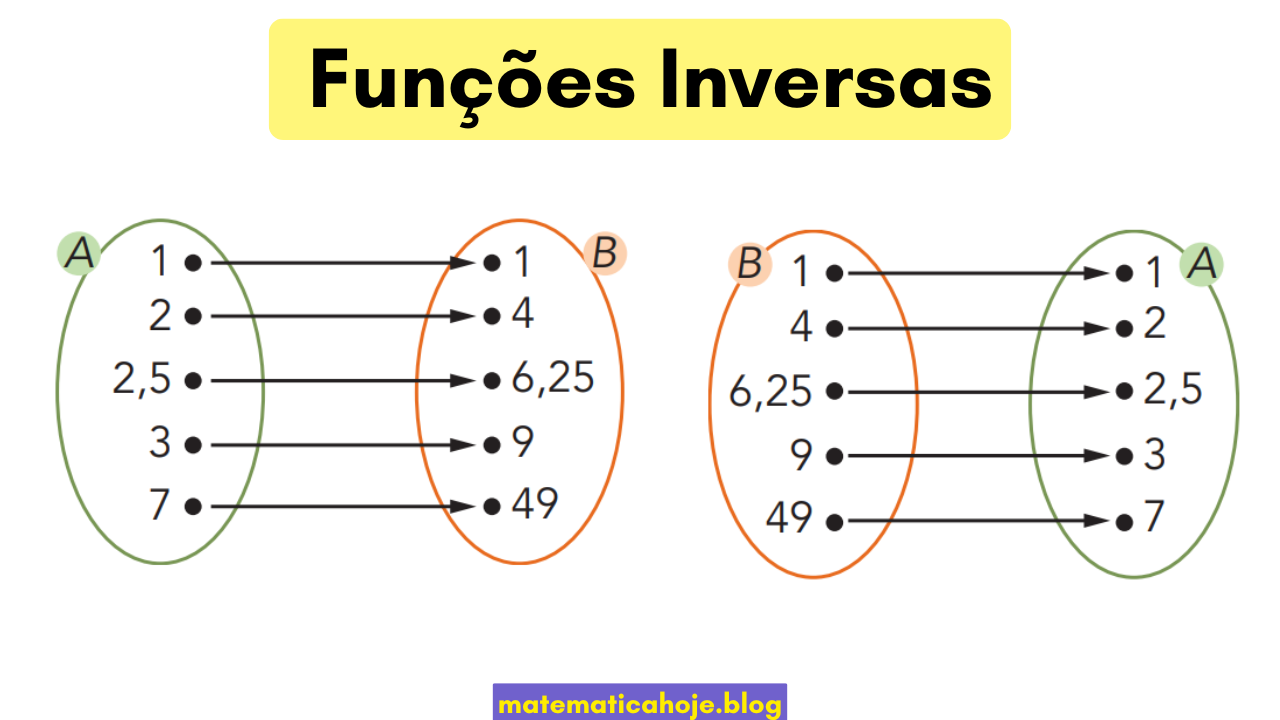
Condições e propriedades

Existência \[ f^{-1}\ \text{é função} \iff f \text{ é bijetiva no domínio considerado}. \] (Se não for, restrinja o domínio para torná-la bijetiva.)

Composição \[ f^{-1}(f(x))=x \ \ (\forall x\in A)\qquad\text{e}\qquad f(f^{-1}(y))=y \ \ (\forall y\in B). \]

Domínio e imagem trocam \[ D\!\left(f^{-1}\right)=\operatorname{Im}(f),\qquad \operatorname{Im}\!\left(f^{-1}\right)=D(f). \]

Gráfico: o gráfico de \(f^{-1}\) é o de \(f\) refletido na reta \(y=x\).
Teste da reta horizontal: se toda reta horizontal corta o gráfico de \(f\) no máx. 1 ponto no intervalo, \(f\) é injetiva ali \(\Rightarrow\) inversa (como função) existe nesse intervalo.

Passo a passo para achar \(f^{-1}\)

Escreva \(y=f(x)\).
Troque \(x\) por \(y\) e \(y\) por \(x\).
Resolva para \(y\). O resultado é \(f^{-1}(x)\).
Ajuste domínio/contradomínio se necessário (trocam de lugar).

📘 Dica de estudo: veja o eBook Fórmulas Matemática (com tabelas de inversas mais comuns).

Exemplos resolvidos

1) Linear

\(f(x)=3x-7\) (\(\mathbb{R}\to\mathbb{R}\)).

\(y=3x-7\Rightarrow x=\dfrac{y+7}{3}\Rightarrow f^{-1}(x)=\dfrac{x+7}{3}\). Bijeção, logo \(D(f^{-1})=\mathbb{R}\) e \(\operatorname{Im}(f^{-1})=\mathbb{R}\).

2) Exponencial e log

\(g(x)=e^x:\ \mathbb{R}\to(0,\infty)\). Inversa \(g^{-1}(x)=\ln x:\ (0,\infty)\to\mathbb{R}\). Domínios/Imagens trocam perfeitamente.

3) Quadrática com restrição

\(h(x)=x^2\) não é injetiva em \(\mathbb{R}\). Restrinja a \(x\ge0\): \(h:[0,\infty)\to[0,\infty)\) fica bijetiva e \(h^{-1}(x)=\sqrt{x}\).

4) Valor absoluto com restrição

\(p(x)=|x-2|\) não é injetiva em \(\mathbb{R}\). Em \(x\ge2\), \(p(x)=x-2\Rightarrow p^{-1}(x)=x+2\) (domínio da inversa: \([0,\infty)\)). Em \(x\le2\), \(p(x)=2-x\Rightarrow p^{-1}(x)=2-x\) (domínio da inversa: \([0,\infty)\)).

5) Racional (Möbius)

\(F(x)=\dfrac{ax+b}{cx+d}\) com \(ad-bc\neq0\). Troque \(x\leftrightarrow y\) e isole \(y\):

\[ x=\frac{ay+b}{cy+d}\ \Rightarrow\ x(cy+d)=ay+b \ \Rightarrow\ y=\frac{dx-b}{-cx+a}. \] Domínios: \(x\neq -d/c\) em \(F\) e \(x\neq a/c\) em \(F^{-1}\).

Tabela rápida (originais ↔ inversas)

Pares clássicos
\(f(x)\)	Domínio \(\to\) Imagem	\(f^{-1}(x)\)	Domínio \(\to\) Imagem
\(ax+b\) (\(a\ne0\))	\(\mathbb{R}\to\mathbb{R}\)	\(\dfrac{x-b}{a}\)	\(\mathbb{R}\to\mathbb{R}\)
\(e^x\)	\(\mathbb{R}\to(0,\infty)\)	\(\ln x\)	\((0,\infty)\to\mathbb{R}\)
\(x^n\) (\(n\) ímpar)	\(\mathbb{R}\to\mathbb{R}\)	\(\sqrt[n]{x}\)	\(\mathbb{R}\to\mathbb{R}\)
\(x^2\) com \(x\ge0\)	\([0,\infty)\to[0,\infty)\)	\(\sqrt{x}\)	\([0,\infty)\to[0,\infty)\)
\(\ln x\)	\((0,\infty)\to\mathbb{R}\)	\(e^x\)	\(\mathbb{R}\to(0,\infty)\)
\(\dfrac{ax+b}{cx+d}\)	\(\mathbb{R}\!\setminus\!\{-d/c\}\to\mathbb{R}\!\setminus\!\{a/c\}\)	\(\dfrac{dx-b}{-cx+a}\)	\(\mathbb{R}\!\setminus\!\{a/c\}\to\mathbb{R}\!\setminus\!\{-d/c\}\)

➡️ Praticar inversas no Banco de Questões

Exercícios (múltipla escolha) com solução

1) Encontre a inversa (quando existir) de \(f(x)=5x+2\) em \(\mathbb{R}\to\mathbb{R}\).

\(f^{-1}(x)=\dfrac{x+2}{5}\)
\(f^{-1}(x)=\dfrac{x-2}{5}\)
\(f^{-1}(x)=5x-2\)
Não existe inversa

Ver solução

\(y=5x+2\Rightarrow x=\dfrac{y-2}{5}\Rightarrow f^{-1}(x)=\dfrac{x-2}{5}\). Alternativa (b).

2) \(g(x)=x^2\) é invertível como função \(\mathbb{R}\to\mathbb{R}\)?

Sim, inversa \(\sqrt{x}\)
Sim, inversa \(\pm\sqrt{x}\)
Não, pois não é injetiva em \(\mathbb{R}\)
Sim, inversa \(|x|\)

Ver solução

Não passa no teste da reta horizontal em \(\mathbb{R}\). Alternativa (c). Em \([0,\infty)\) passa a ser invertível.

3) A inversa de \(h(x)=\ln(x-1)\) com domínio \((1,\infty)\) é:

\(h^{-1}(x)=e^x-1\)
\(h^{-1}(x)=e^{x+1}\)
\(h^{-1}(x)=\ln(x)+1\)
\(h^{-1}(x)=e^x+1\)

Ver solução

\(y=\ln(x-1)\Rightarrow x-1=e^y\Rightarrow x=e^y+1\Rightarrow h^{-1}(x)=e^x+1\). Alternativa (d).

4) \(p(x)=\dfrac{2x-3}{x+1}\). Qual é \(p^{-1}(x)\)?

\(\dfrac{3x+2}{1-x}\)
\(\dfrac{3x+2}{x-1}\)
\(\dfrac{x+3}{2-x}\)
\(\dfrac{x+3}{x-2}\)

Ver solução

\(x=\dfrac{2y-3}{y+1}\Rightarrow x(y+1)=2y-3\Rightarrow xy+x=2y-3\Rightarrow y(x-2)=-x-3\Rightarrow y=\dfrac{-x-3}{x-2}=\dfrac{x+3}{2-x}\). Alternativa (c).

5) O gráfico de \(f^{-1}\) pode ser obtido a partir do gráfico de \(f\) por: