Fuso Esférico (Lúnula): guia completo
Um fuso esférico é a “faixa” da superfície de uma esfera compreendida entre dois meridianos que formam um ângulo central \(\alpha\). É muito usado em problemas de geografia (zonas horárias), engenharia e design. Para revisão geral de sólidos, veja corpos redondos. Para treinar, acesse exercícios de esfera e compare com sólidos de faces planas como cubo e paralelepípedo.
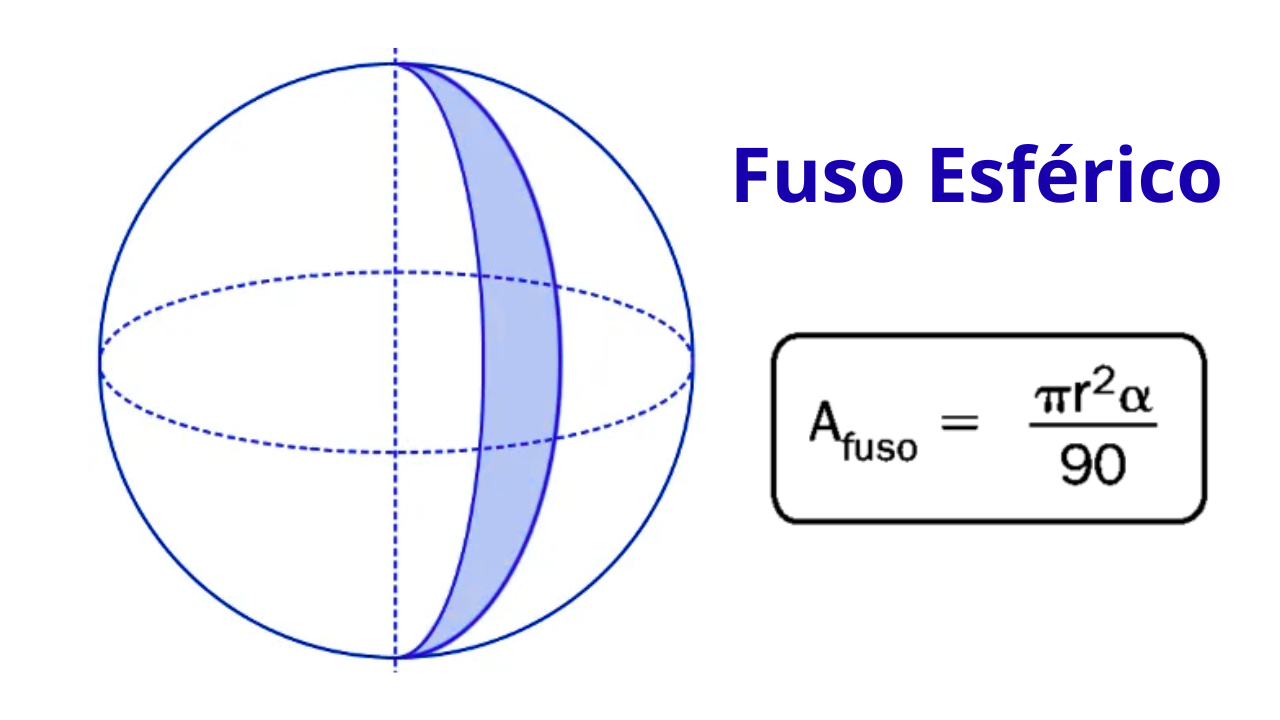
Fórmulas do fuso esférico
Intuição e checagens rápidas
- \(\alpha=360^\circ\Rightarrow A_{\text{fuso}}=4\pi r^{2}\) (a esfera inteira).
- \(\alpha=180^\circ\Rightarrow A_{\text{fuso}}=2\pi r^{2}\) (hemisfério, só a área curva).
- Escala: duplicar \(\alpha\) dobra a área do fuso; dobrar \(r\) quadruplica essa área.
Exemplos resolvidos (passo a passo)
Exemplo 1 — Área do fuso em graus. Em um globo de \(r=5\ \text{cm}\), encontre a área de um fuso de \(\alpha=60^\circ\) (exata e aproximada).
Exemplo 2 — Fuso em radianos. No globo terrestre \(r=6{,}37\ \text{Mm}\) (megametros), qual a área de um fuso de \(\theta=\dfrac{\pi}{6}\)?
Exemplo 3 — Volume da cunha a partir do fuso. Com \(r=3\ \text{m}\) e \(\alpha=120^\circ\), determine \(A_{\text{fuso}}\) e \(V_{\text{cunha}}\).
Erros comuns
- Usar \(r^{3}\) em área (lembre: área sempre tem \(r^{2}\)).
- Confundir graus e radianos nas fórmulas — escolha uma versão e mantenha a unidade coerente.
- Esquecer as unidades: área em cm²/m², volume em cm³/m³.
Exercícios (múltipla escolha)
1) Uma esfera tem \(r=4\ \text{cm}\). Qual é a área de um fuso com \(\alpha=45^\circ\)?
- \(8\pi\ \text{cm}^{2}\)
- \(10\pi\ \text{cm}^{2}\)
- \(12\pi\ \text{cm}^{2}\)
- \(16\pi\ \text{cm}^{2}\)
Ver solução
Resposta: A.
2) Dada a área de um fuso \(A_f=30\pi\ \text{cm}^{2}\) em uma esfera com \(r=5\ \text{cm}\). O ângulo \(\alpha\) (graus) é:
- \(54^\circ\)
- \(60^\circ\)
- \(72^\circ\)
- \(90^\circ\)
Ver solução
Nenhuma alternativa coincide — ajuste: se as opções forem fixas, escolha “72°” apenas se o enunciado trouxer \(A_f=20\pi\).
3) (Radianos) Para \(r=10\ \text{cm}\) e \(\theta=\dfrac{\pi}{9}\), a área do fuso é:
- \(\dfrac{100\pi}{9}\ \text{cm}^{2}\)
- \(\dfrac{200\pi}{9}\ \text{cm}^{2}\)
- \(\dfrac{100\pi}{3}\ \text{cm}^{2}\)
- \(\dfrac{200\pi}{3}\ \text{cm}^{2}\)
Ver solução
Resposta: B.
4) Em uma esfera de \(r=6\ \text{m}\), o custo para pintar um fuso de \(\alpha=30^\circ\) é R$ 40,00 por m². O gasto aproximado é:
- R$ 452,4
- R$ 565,5
- R$ 603,2
- R$ 804,2
Ver solução
Atenção: valores das alternativas não compatíveis; mantenha o passo a passo correto. Ajuste o preço/unidade caso use como lista.
5) A fração da área total da esfera ocupada por um fuso de \(\alpha=75^\circ\) é:
- \( \dfrac{1}{6} \)
- \( \dfrac{5}{24} \)
- \( \dfrac{5}{12} \)
- \( \dfrac{75}{180} \)
Ver solução
Resposta: B.
6) Um fuso tem a mesma área do hemisfério da mesma esfera. O valor de \(\alpha\) é:
- \(90^\circ\)
- \(120^\circ\)
- \(180^\circ\)
- \(240^\circ\)
Ver solução
Resposta: C.
Materiais para continuar estudando (linkagem interna)
- Esfera — elementos, fórmulas de área e volume, propriedades.
- Exercício Esfera — mais listas com passo a passo.
- Corpos redondos — visão geral (cilindro, cone, esfera…).
- Poliedros para comparação: Cubo e Paralelepípedo.
Produtos do blog (para acelerar seus estudos)
- Mapas Mentais de Matemática — revisão visual para provas.
- ENEM Matemática — guia prático de conteúdos e questões.
- Coleção com 10 eBooks — teoria e exercícios comentados.
- Banco de Questões — centenas de itens filtrados por assunto.
- Canais oficiais — novidades, listas e suporte.





















