Interseção de Retas
A interseção de retas é o ponto comum a duas retas no plano cartesiano. Em álgebra, é a solução do sistema formado por suas equações. Tópico recorrente no ENEM, vestibulares e concursos.
1) Modelos de equação da reta
- Forma reduzida: \(y=ax+b\)
- Forma geral: \(Ax+By+C=0\) (com \(A,B\) não simultaneamente nulos)
2) Fórmula rápida para \(y=ax+b\)
Sejam \(r:\,y=ax+b\) e \(s:\,y=cx+d\) com \(a\neq c\). O ponto \(P(x^*,y^*)\) é:
- Se \(a=c\) e \(b\neq d\): paralelas (sem interseção).
- Se \(a=c\) e \(b=d\): coincidentes (infinitas soluções).
3) Métodos algébricos
- Igualação: iguale as expressões de \(y\) e resolva \(x\).
- Substituição: isole uma variável e substitua na outra equação.
- Eliminação: combine equações para eliminar uma variável.
📘 Todas as fórmulas, num só lugar
Baixe o eBook Fórmulas Matemática e revise funções, geometria, estatística e muito mais.
Baixar eBook4) Exemplo 1 — Igualação (com análise geométrica)
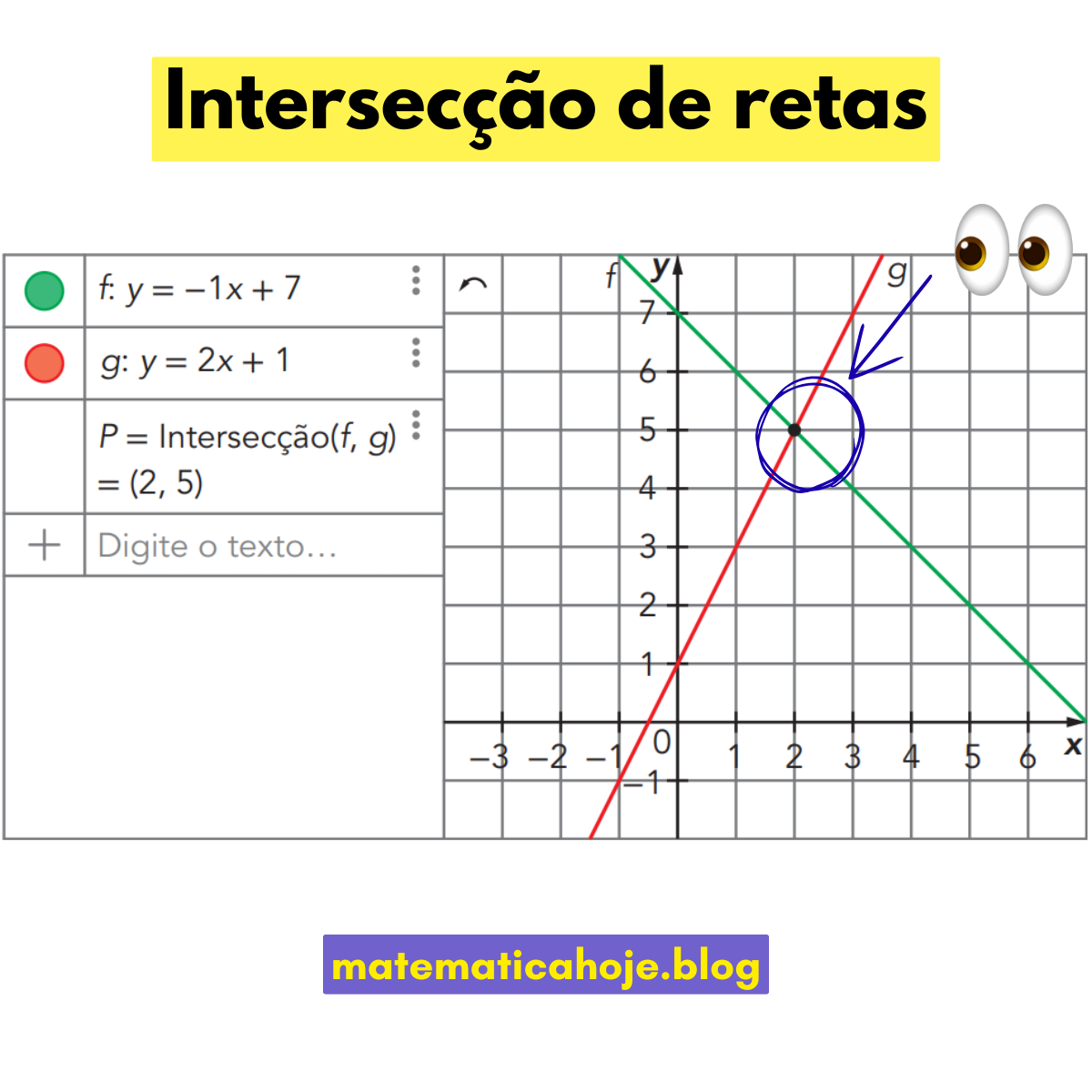
Enunciado: No plano cartesiano, considere as retas \(f:\,y=-x+7\) e \(g:\,y=2x+1\).
a) Verifique se são concorrentes, paralelas ou coincidentes, justificando pela comparação dos coeficientes angulares e lineares.
b) Determine o ponto de interseção \(P(x,y)\) por igualação e confirme o resultado em cada equação.
Ver solução
a) Inclinações diferentes (\(-1\) e \(2\)) ⇒ retas concorrentes.
b) \(-x+7=2x+1\)
\(6=3x \Rightarrow x=2\)
\(y=2x+1=2\cdot2+1=5\)
P(2,5).
5) Exemplo 2 — Fórmula direta (checagem por substituição)
Enunciado: Determine a interseção das retas \(r:\,y=3x-4\) e \(s:\,y=-x+8\) usando a fórmula direta para \(y=ax+b\). Em seguida, substitua as coordenadas obtidas nas duas equações para validar o resultado.
Ver solução
\(x^*=\dfrac{8-(-4)}{3-(-1)}=\dfrac{12}{4}=3\)
\(y^*=3\cdot3-4=5\)
Checando: em \(s\), \(-3+8=5\) ✔️
P(3,5).
6) Exemplo 3 — Eliminação (forma geral + conversão)
Enunciado: Resolva o sistema \(\begin{cases}2x+3y=7\\ -x+y=1\end{cases}\) pelo método da eliminação. Depois, escreva as duas retas na forma reduzida \(y=ax+b\) e confirme o ponto de interseção por leitura direta.
Ver solução
Da 2ª: \(y=1+x\)
Na 1ª: \(2x+3(1+x)=7 \Rightarrow 5x=4 \Rightarrow x=\dfrac{4}{5}\)
\(y=1+\dfrac{4}{5}=\dfrac{9}{5}\)
Formas reduzidas: \(y=-\tfrac{2}{3}x+\tfrac{7}{3}\) e \(y=x+1\).
P\(\left(\dfrac{4}{5},\dfrac{9}{5}\right)\).
7) Exercícios propostos (com soluções no abre/fecha)
1) Interpretação + cálculo. Em \(\mathbb{R}^2\), as retas \(r:\,y=4x-3\) e \(s:\,y=x+6\) modelam duas tendências lineares.
a) Classifique a posição relativa (concorrentes/paralelas/coincidentes).
b) Calcule o ponto de interseção \(P\) e apresente as contas.
Ver solução
a) Inclinações \(4\) e \(1\) ⇒ concorrentes.
b) \(4x-3=x+6 \Rightarrow 3x=9 \Rightarrow x=3\)
\(y=x+6=9\)
P(3,9).
2) Forma geral + verificação. Resolva o sistema \(\begin{cases}3x-2y=1\\ x+y=5\end{cases}\). Depois, verifique o resultado substituindo as coordenadas encontradas em ambas as equações.
Ver solução
Da 2ª: \(y=5-x\)
Substituindo: \(3x-2(5-x)=1 \Rightarrow 5x=11 \Rightarrow x=\tfrac{11}{5}\)
\(y=5-\tfrac{11}{5}=\tfrac{14}{5}\)
Verificação: \(3\cdot\tfrac{11}{5}-2\cdot\tfrac{14}{5}=\tfrac{33-28}{5}=\tfrac{5}{5}=1\) ✔️
P\(\left(\tfrac{11}{5},\tfrac{14}{5}\right)\).
3) Classificação. As retas \(y=2x+1\) e \(y=2x-3\) representam duas funções afins. Determine se há interseção. Caso não haja, explique geometricamente.
Ver solução
Mesmo coeficiente angular (\(a=2\)) e interceptos diferentes ⇒ paralelas. Não se intersectam.
4) Parâmetro. Para quais valores de \(k\) as retas \(y=5x+k\) e \(y=5x-2\) são:
a) coincidentes; b) paralelas não coincidentes; c) Existe interseção quando \(k=0\)? Justifique.
Ver solução
a) Coincidentes se interceptos iguais: \(k=-2\).
b) Paralelas para qualquer \(k\neq -2\) (mesmo \(a\), interceptos distintos).
c) Para \(k=0\): \(y=5x\) e \(y=5x-2\) são paralelas ⇒ não há interseção.
5) Reta por dois pontos + outra na forma reduzida. A reta \(r\) passa por \(A(1,3)\) e \(B(5,11)\). A reta \(s\) é dada por \(y=-x+8\). Determine a lei de \(r\) e o ponto de interseção \(r\cap s\).
Ver solução
\(a_r=\dfrac{11-3}{5-1}=\dfrac{8}{4}=2\)
Usando \(A\): \(3=2\cdot1+b \Rightarrow b=1\) ⇒ \(r:\,y=2x+1\)
Interseção com \(s\): \(2x+1=-x+8 \Rightarrow 3x=7 \Rightarrow x=\tfrac{7}{3}\)
\(y=2\cdot\tfrac{7}{3}+1=\tfrac{14}{3}+1=\tfrac{17}{3}\)
P\(\left(\tfrac{7}{3},\tfrac{17}{3}\right)\).
6) Problema aplicado (ponto de equilíbrio). Dois planos de assinatura cobram conforme a quantidade de horas \(q\) utilizada no mês:
Plano A: \(C_A(q)=2{,}40\,q+12\). Plano B: \(C_B(q)=3{,}00\,q+6\).
a) Encontre o valor de \(q\) em que os planos têm o mesmo custo (interseção das retas).
b) Qual é esse custo?
Ver solução
Igualando: \(2{,}40q+12=3{,}00q+6\)
\(12-6=0{,}60q \Rightarrow q=10\)
Custo: \(C_A(10)=2{,}40\cdot10+12=36\) (mesmo para \(C_B\)).
Ponto de equilíbrio: \(q=10\) horas; custo R$ 36,00.