Teste da Segunda Derivada — Máximos, Mínimos e Concavidade
O Teste da Segunda Derivada permite classificar pontos críticos de \(f\) usando o sinal de \(f”\) e, de quebra, entender a concavidade do gráfico.
1) Teorema (Teste da Segunda Derivada)
Seja \(f\) duas vezes derivável e \(c\) um ponto crítico tal que \(f'(c)=0\). Se \(f”\) é contínua em torno de \(c\), então:
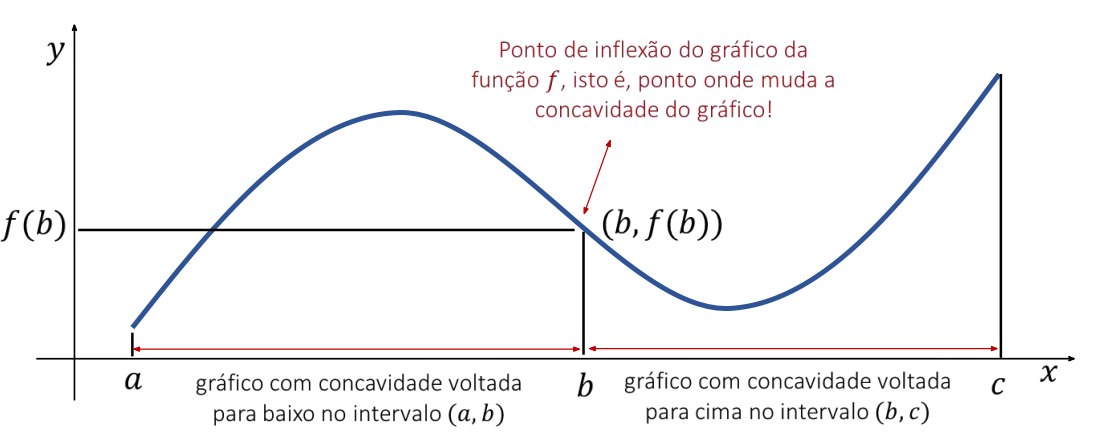
Concavidade: \(f”(x)>0\) indica concavidade para cima; \(f”(x)<0\) indica concavidade para baixo. Se \(f”\) muda de sinal em \(x=a\), \(a\) é candidato a inflexão (exige continuidade de \(f’\)).
2) Roteiro rápido
- Encontre \(D_f\) (domínio).
- Calcule \(f'(x)\) e resolva \(f'(x)=0\) (pontos estacionários).
- Calcule \(f”(x)\) e avalie \(f”(c)\) nos pontos críticos.
- Classifique com o teste acima e calcule \(f(c)\).
- Se \(f”(c)=0\) ou não existir, use o Teste da Primeira Derivada.
3) Exemplos resolvidos
Exemplo A — Quadrática
\(f(x)=x^2+2x-4\).
Ver solução
Logo \(c=-1\) é mínimo local e
| Ponto | Classificação | Valor |
|---|---|---|
| \(x=-1\) | Mínimo | \(f(-1)=-5\) |
Exemplo B — Cúbica
\(f(x)=x^3-3x\).
Ver solução
\(f”(-1)=-6<0\Rightarrow\) máximo em \((-1,2)\); \(f”(1)=6>0\Rightarrow\) mínimo em \((1,-2)\).
| Ponto | Classificação | Valor |
|---|---|---|
| \(x=-1\) | Máximo | \(f(-1)=2\) |
| \(x=1\) | Mínimo | \(f(1)=-2\) |
Exemplo C — Exponencial − linear
\(f(x)=e^x-2x\).
Ver solução
Mínimo local em \(x=\ln 2\).
Exemplo D — Caso inconclusivo
\(f(x)=x^4\).
Ver solução
O teste é inconclusivo. Pelo sinal de \(f’\) (ou pelo gráfico), há mínimo em \(x=0\) com \(f(0)=0\).
4) Exercícios propostos (com soluções)
-
\(f(x)=x^4-4x^2+1\). Encontre os pontos críticos, classifique com o teste da segunda derivada e calcule os valores de \(f\).
Mostrar solução
\[ f'(x)=4x^3-8x=4x(x^2-2)=0 \Rightarrow x=0,\ \pm\sqrt2. \] \[ f”(x)=12x^2-8\Rightarrow f”(0)=-8<0,\ f”(\pm\sqrt2)=16>0. \]Logo: máximo em \(x=0\) com \(f(0)=1\); mínimos em \(x=\pm\sqrt2\) com \(f(\pm\sqrt2)=4-8+1=-3\).
-
\(f(x)=\dfrac{x}{x^2+1}\). Classifique os críticos via \(f”\).
Mostrar solução
\[ f'(x)=\frac{1-x^2}{(x^2+1)^2}=0 \Rightarrow x=\pm1. \] \[ f”(x)=\frac{2x(x^2-3)}{(x^2+1)^3}\Rightarrow f”(1)=-\tfrac12<0,\ f”(-1)=\tfrac12>0. \]Máximo em \(x=1\) com \(f(1)=\tfrac12\); mínimo em \(x=-1\) com \(f(-1)=-\tfrac12\).
-
\(f(x)=e^{2x}-3e^x\). Determine o crítico e classifique.
Mostrar solução
\[ f'(x)=e^x(2e^x-3)=0 \Rightarrow e^x=\tfrac32 \Rightarrow x=\ln\tfrac32. \] \[ f”(x)=e^x(4e^x-3)\Rightarrow f”(c)=\tfrac32(6-3)=\tfrac92>0. \]Mínimo em \(x=\ln\tfrac32\) com \(f(c)=(\tfrac32)^2-3(\tfrac32)=-\tfrac{9}{4}\).
-
\(f(x)=\ln x – x\) (domínio \(x>0\)). Use \(f”\) para classificar.
Mostrar solução
\[ f'(x)=\frac{1}{x}-1=0 \Rightarrow x=1,\qquad f”(x)=-\frac{1}{x^2}\Rightarrow f”(1)<0. \]Máximo em \(x=1\) com \(f(1)=-1\).
-
\(f(x)=x^3-3x^2+2\). Classifique todos os críticos.
Mostrar solução
\[ f'(x)=3x^2-6x=3x(x-2)=0 \Rightarrow x=0,2;\qquad f”(x)=6x-6. \] \[ f”(0)=-6<0 \Rightarrow \text{máximo},\quad f(0)=2. \qquad f”(2)=6>0 \Rightarrow \text{mínimo},\quad f(2)=-2. \]
5) Resumo rápido
Classificação em 1 linha: \(f”(c)<0\) ⇒ máximo; \(f''(c)>0\) ⇒ mínimo; \(f”(c)=0\) ⇒ teste inconclusivo (use o da 1ª derivada).
Para concavidade: estude o sinal de \(f”(x)\) por intervalos. Mudança de sinal de \(f”\) em \(a\) (com \(f’\) contínua) sugere inflexão.













