Operações com Números Inteiros — Guia Completo com Exemplo Passo a Passo
Atualizado em 23 de agosto de 2025 • Leitura ~25 min • Material didático, visual e estratégico
Revisão rápida: o que são inteiros
O conjunto dos números inteiros é \(\mathbb{Z}=\{\ldots,-3,-2,-1,0,1,2,3,\ldots\}\). Ele estende os naturais incorporando negativos e permite resolver problemas de saldo, temperatura, altitudes, entre outros.
Para ver onde os inteiros se encaixam nos demais conjuntos, confira Conjuntos Numéricos e o panorama em Números Reais. Para operações gerais, veja também Operações Numéricas e a versão para números naturais.
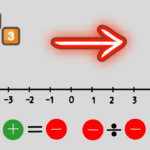
Reta numérica, módulo e valor absoluto
Na reta numérica os valores aumentam para a direita e diminuem para a esquerda. O módulo ou valor absoluto de \(a\) é a distância de \(a\) até o zero:
Ex.: \(|-7|=7\)
Ex.: \(|4|=4\)
Regras de sinais
Somar/Subtrair inteiros
- Sinais iguais (somar módulos e manter o sinal): \(-8)+(-3)=-11\).
- Sinais diferentes (subtrair módulos e manter o sinal do maior módulo): \(15+(-9)=6\).
- Subtração: transforme em soma do oposto: \(a-b=a+(-b)\).
Multiplicar/Dividir inteiros
- \((+)\times(+)=+\), \((−)\times(−)=+\)
- \((+)\times(−)=−\), \((−)\times(+)=−\)
- As mesmas regras valem para a divisão.
Propriedades fundamentais (versão responsiva)
Em \(\mathbb{Z}\), algumas propriedades valem para certas operações. Em vez de tabela larga, apresentamos em blocos (melhor em telas menores):
➕ Adição
- Comutativa: Sim → \(a+b=b+a\)
- Associativa: Sim → \((a+b)+c=a+(b+c)\)
- Neutro: \(0\) → \(a+0=a\)
- Distributiva: não se aplica (quem distribui é a multiplicação).
✖ Multiplicação
- Comutativa: Sim → \(ab=ba\)
- Associativa: Sim → \((ab)c=a(bc)\)
- Neutro: \(1\) → \(a\cdot1=a\)
- Distributiva: Sim → \(a(b+c)=ab+ac\)
➖ Subtração
- Comutativa/Associativa: Não.
- Neutro: não definido. Use \(a-b=a+(-b)\).
➗ Divisão
- Comutativa/Associativa: Não.
- Fechamento: em \(\mathbb{Z}\) a divisão nem sempre é inteira (ex.: \(1\div 2\) não está em \(\mathbb{Z}\)).
Ordem de operações (prioridades)
- Parênteses e colchetes
- Potências e raízes
- Multiplicações e divisões (da esquerda para a direita)
- Adições e subtrações (da esquerda para a direita)
Para um panorama com decimais, frações e raízes, veja Operações Numéricas.
Exemplos práticos resolvidos (passo a passo)
1) Soma e subtração com sinais mistos
Calcule: \(-18 + 35 – (-12) + 7\)
- Troque “menos com menos”: \(-(-12)=+12\).
- \(-18 + 35 = 17\).
- \(17 + 12 = 29\).
- \(29 + 7 = 36\).
Resposta: \(36\).
2) Expressão com parênteses
Calcule: \(6 + 4\cdot(9-5)^2 \div 8\)
- \(9-5=4\).
- \(4^2=16\).
- \(4\cdot16=64\) e \(64\div 8=8\).
- \(6+8=14\).
Resposta: \(14\).
3) Multiplicação e divisão com sinais
Calcule: \((-6)\cdot 4 \div (-3)\)
- \((-6)\cdot 4=-24\) (sinais diferentes → negativo).
- \(-24\div(-3)=8\) (sinais iguais → positivo).
Resposta: \(8\).
4) Potenciação com base negativa
Calcule: \((-3)^4\) e \(-3^4\)
- \((-3)^4=(−3)\cdot(−3)\cdot(−3)\cdot(−3)=81\) (expoente par → positivo).
- \(-3^4=-(3^4)=-81\) (o expoente atinge só o 3).
Respostas: \(81\) e \(-81\).
5) Valor absoluto em expressão
Calcule: \(|-5| + |3-10| – |{-2}|\)
- \(|-5|=5\).
- \(3-10=-7\Rightarrow |{-7}|=7\).
- \(|-2|=2\).
- Total: \(5+7-2=10\).
Resposta: \(10\).
6) Problema contextual (saldo)
Um jogador tinha \(-27\) pontos. Ganhou \(+18\), perdeu \(-12\) e depois ganhou \(+25\). Qual o saldo final?
- \(-27+18=-9\).
- \(-9-12=-21\).
- \(-21+25=4\).
Resposta: \(4\) pontos.
Exercícios propostos
- \(-27 + 15 – ( -9 ) + 4\)
- \(12 – [\,7 – ( -5 )\,]\)
- \((-8)\cdot(-5) \div 10\)
- \((−2)^5 + (−2)^4\)
- \(|{-11}| – |4-13| + |0|\)
- \(8 + 3 \cdot \big( 10 – 4^2 \big) \div 2\)
Gabarito comentado
1) \(-27+15=-12\); \(-12-(-9)= -3\); \(-3+4=1\). Resp.: 1.
3) \((-8)\cdot(-5)=40\); \(40\div10=4\). Resp.: 4.
4) \((−2)^5 = −32\); \((−2)^4=16\) ⇒ soma \(−16\). Resp.: −16.
5) \(|{-11}|=11\); \(4-13=-9\Rightarrow |{-9}|=9\); \(|0|=0\). \(11-9+0=2\). Resp.: 2.
6) \(4^2=16\Rightarrow 10-16=-6\); \(3\cdot(-6)=-18\); \(-18\div2=-9\); \(8+(-9)=-1\). Resp.: −1.