Pontos Notáveis do Triângulo

Pontos Notáveis do Triângulo: baricentro, incentro, circuncentro e ortocentro

Pontos Notáveis do Triângulo

Baricentro, Incentro, Circuncentro e Ortocentro — definições, e exercícios resolvidos com passos em linhas separadas.

Geometria PlanaTriângulosPropriedadesExercícios com solução

O que são “pontos notáveis”?

Chamamos de pontos notáveis do triângulo os pontos definidos pela concorrência (interseção) de segmentos ou retas especiais. Os quatro clássicos são:

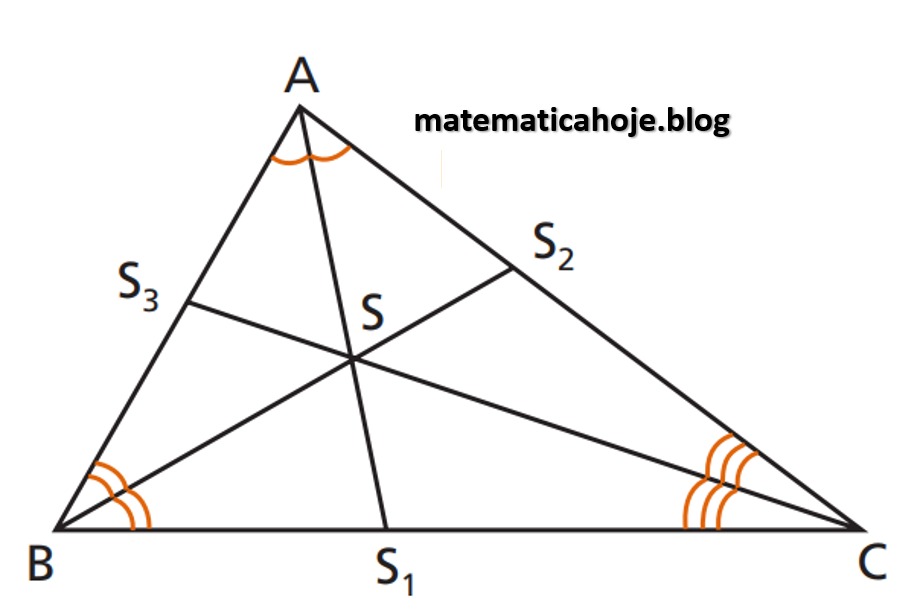
Baricentro (G): encontro das medianas. Medianas e baricentro.
Incentro (I): encontro das bissetrizes internas. Bissetrizes e incentro.
Circuncentro (O): encontro das mediatrizes dos lados. Base de congruência.
Ortocentro (H): encontro das alturas. Alturas e ortocentro.

Cada ponto notável tem interpretação geométrica (centro de massa, círculo inscrito, círculo circunscrito, etc.) e posição que varia conforme o tipo de triângulo.

Baricentro (G) — encontro das medianas

Definição. Interseção das três medianas do triângulo.

Propriedade. Divide cada mediana na razão 2:1 (do vértice para o baricentro é o dobro).

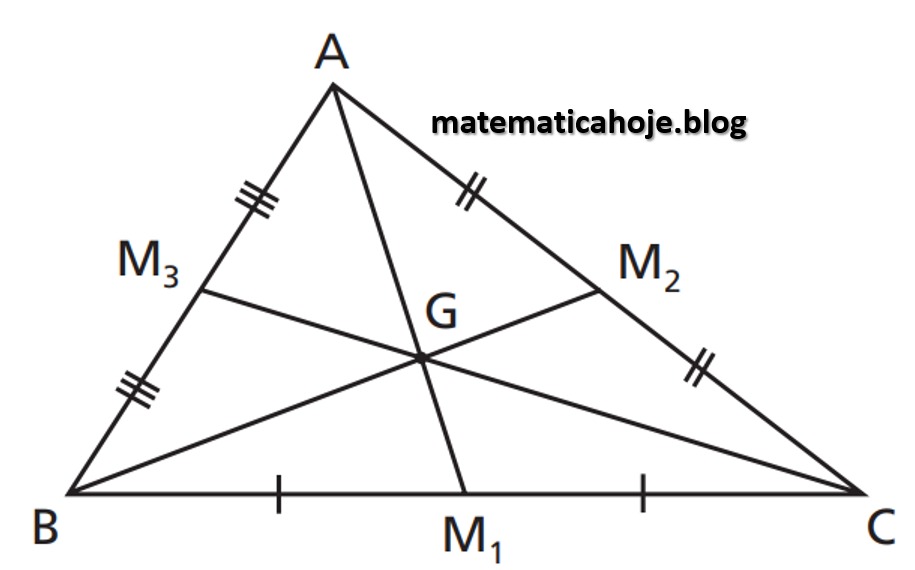
Triângulo ABC com medianas concorrendo no baricentro G

Nota: o baricentro é o centro de gravidade do triângulo.

Exercício 1 — Verdadeiro ou falso (conceitos)

I) O baricentro é sempre interno. II) É o encontro das mediatrizes. III) É equidistante dos vértices. Assinale a correta (A) I (B) II (C) III (D) I e III (E) Todas.

Ver solução

I) Verdadeira.
II) Falsa — encontro das mediatrizes define o circuncentro.
III) Falsa — o ponto equidistante dos vértices é o circuncentro.

Gabarito: A.

Exercício 2 — Baricentro no plano cartesiano

Dado $A(-1,-2)$, $B(3,5)$ e $C(4,-3)$, determine o baricentro $G$.

Ver solução

No plano, o baricentro é a média das coordenadas:

$$ G\left(\frac{x_A+x_B+x_C}{3},\,\frac{y_A+y_B+y_C}{3}\right) $$
$$ = \left(\frac{-1+3+4}{3},\,\frac{-2+5-3}{3}\right) $$
$$ = \left(\frac{6}{3},\,\frac{0}{3}\right) $$
$$ = (2,0). $$

Gabarito: $G(2,0)$.

Leitura: medianas e baricentro • exercícios

Incentro (I) — encontro das bissetrizes internas

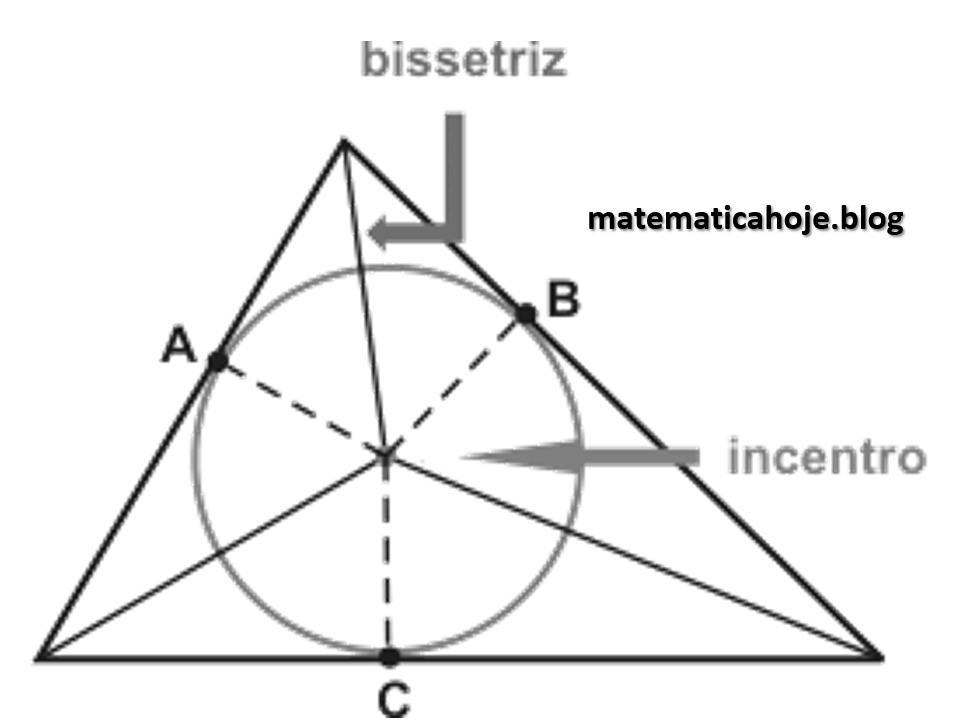
Definição. Interseção das três bissetrizes internas.

Triângulo com bissetrizes internas concorrendo no incentro I

Propriedade. É equidistante dos lados (centro da circunferência inscrita).

Circunferência inscrita tocando os três lados

Exercício 1 — Raio da inscrita em triângulo retângulo

Num triângulo retângulo com catetos 9 e 12, determine o raio $r$ da inscrita.

Ver solução

$$ c=\sqrt{9^2+12^2}=15 $$
$$ A=\frac{9\cdot12}{2}=54 $$
$$ s=\frac{9+12+15}{2}=18 $$
$$ r=\frac{A}{s}=\frac{54}{18}=3. $$

Gabarito: $r=3$.

Exercício 2 — Triângulo 13–14–15

Para lados $13$, $14$ e $15$, calcule o raio $r$ do círculo inscrito.

Ver solução

$$ s=\frac{13+14+15}{2}=21 $$
$$ A=\sqrt{s(s-a)(s-b)(s-c)} $$
$$ =\sqrt{21\cdot(21-13)\cdot(21-14)\cdot(21-15)} $$
$$ =\sqrt{21\cdot8\cdot7\cdot6}=\sqrt{7056}=84 $$
$$ r=\frac{A}{s}=\frac{84}{21}=4. $$

Gabarito: $r=4$.

Leitura: bissetrizes e incentro

Circuncentro (O) — encontro das mediatrizes

Definição. Interseção das mediatrizes dos lados.

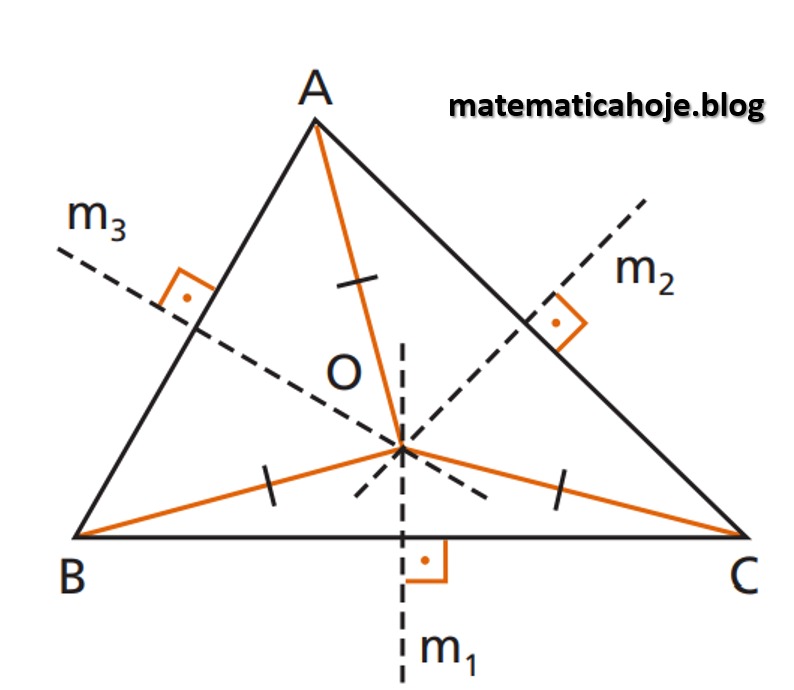
Triângulo com mediatrizes concorrendo no circuncentro O

Propriedade. É equidistante dos vértices (centro da circunferência circunscrita).

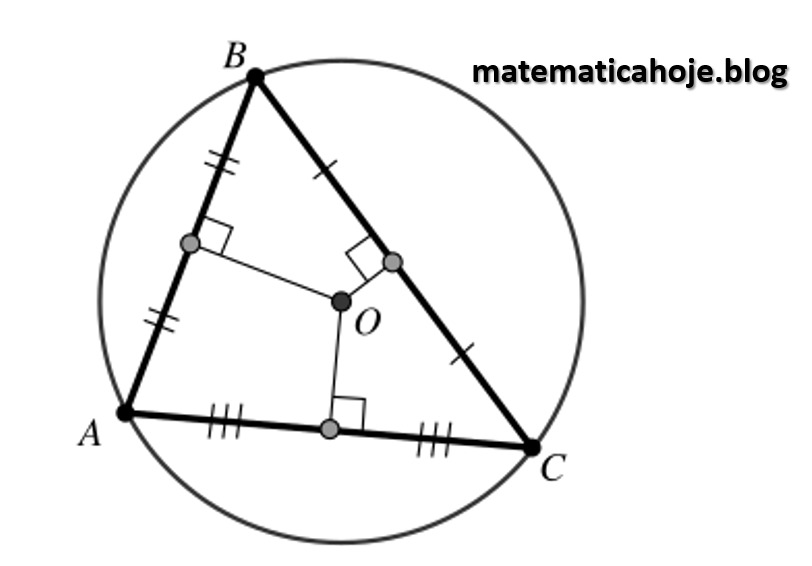
Circunferência circunscrita passando pelos três vértices

Exercício 1 — Triângulo retângulo (coordenadas)

Considere $A(0,0)$, $B(8,0)$, $C(0,6)$. Determine $O$ e o raio $R$.

Ver solução

$$ O=\left(\frac{8+0}{2},\,\frac{0+6}{2}\right)=(4,3) $$
$$ |BC|=\sqrt{(8-0)^2+(0-6)^2} $$
$$ =\sqrt{64+36}=\sqrt{100}=10 $$
$$ R=\frac{|BC|}{2}=\frac{10}{2}=5. $$

Gabarito: $O(4,3)$ e $R=5$.

Exercício 2 — Triângulo equilátero

Num equilátero de lado $a=6$, determine $R$.

Ver solução

$$ R=\frac{a}{\sqrt{3}} $$
$$ =\frac{6}{\sqrt{3}} $$
$$ =2\sqrt{3}. $$

Gabarito: $R=2\sqrt{3}$.

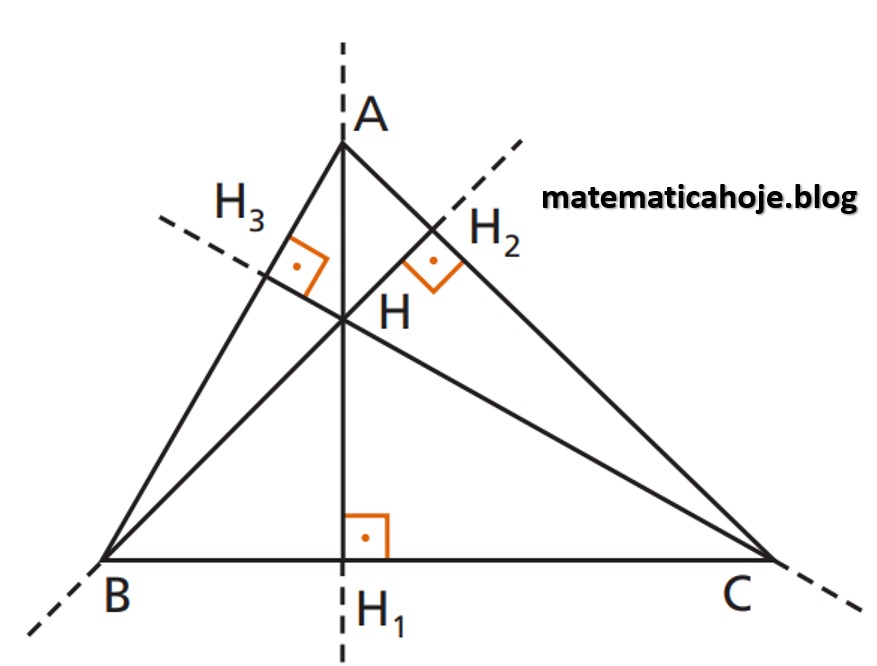
Ortocentro (H) — encontro das alturas

Definição. Interseção das retas-suporte das alturas.

Posição. Acutângulo: interno; Retângulo: o vértice do ângulo reto; Obtusângulo: externo.

Triângulo com alturas concorrendo no ortocentro H

Exercício 1 — Triângulo retângulo

Com $A(0,0)$, $B(6,0)$, $C(0,8)$ (ângulo reto em $A$), determine $H$.

Ver solução

$$ \text{Em triângulo retângulo, } H \text{ coincide com o vértice do ângulo reto.} $$
$$ H=A $$
$$ H=(0,0). $$

Gabarito: $H(0,0)$.

Exercício 2 — Triângulo equilátero

Num equilátero de lado $a$, mostre que $H$ coincide com os demais centros e calcule a distância desse ponto a cada lado.

Ver solução

$$ G=I=O=H \quad (\text{todas as linhas notáveis coincidem}) $$
$$ h=\frac{\sqrt{3}}{2}a $$
$$ r=\frac{h}{3}=\frac{a\sqrt{3}}{6}. $$

Gabarito: Centros coincidem e a distância a cada lado é $r=\dfrac{a\sqrt{3}}{6}$.

Leitura: alturas e ortocentro

Resumo rápido

Baricentro (G): encontro das medianas; razão 2:1; centro de gravidade.
Incentro (I): encontro das bissetrizes internas; equidistante dos lados; círculo inscrito.
Circuncentro (O): encontro das mediatrizes; equidistante dos vértices; círculo circunscrito.
Ortocentro (H): encontro das alturas; posição depende do tipo de triângulo.

Pratique mais: Exercícios – Pontos Notáveis do Triângulo.

Links de produtos do blog

Relacionadas

Relações Métricas no Triângulo Retângulo

Razões Trigonométricas no Triângulo Retângulo

Teorema de Pitágoras

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.