O Teorema da Bissetriz Interna é um resultado importante da Geometria Plana que relaciona a bissetriz de um ângulo interno de um triângulo com os lados opostos. Ele permite calcular segmentos em um triângulo usando apenas proporcionalidade — ferramenta essencial para o ENEM, vestibulares e concursos.
Figura do Teorema da Bissetriz Interna
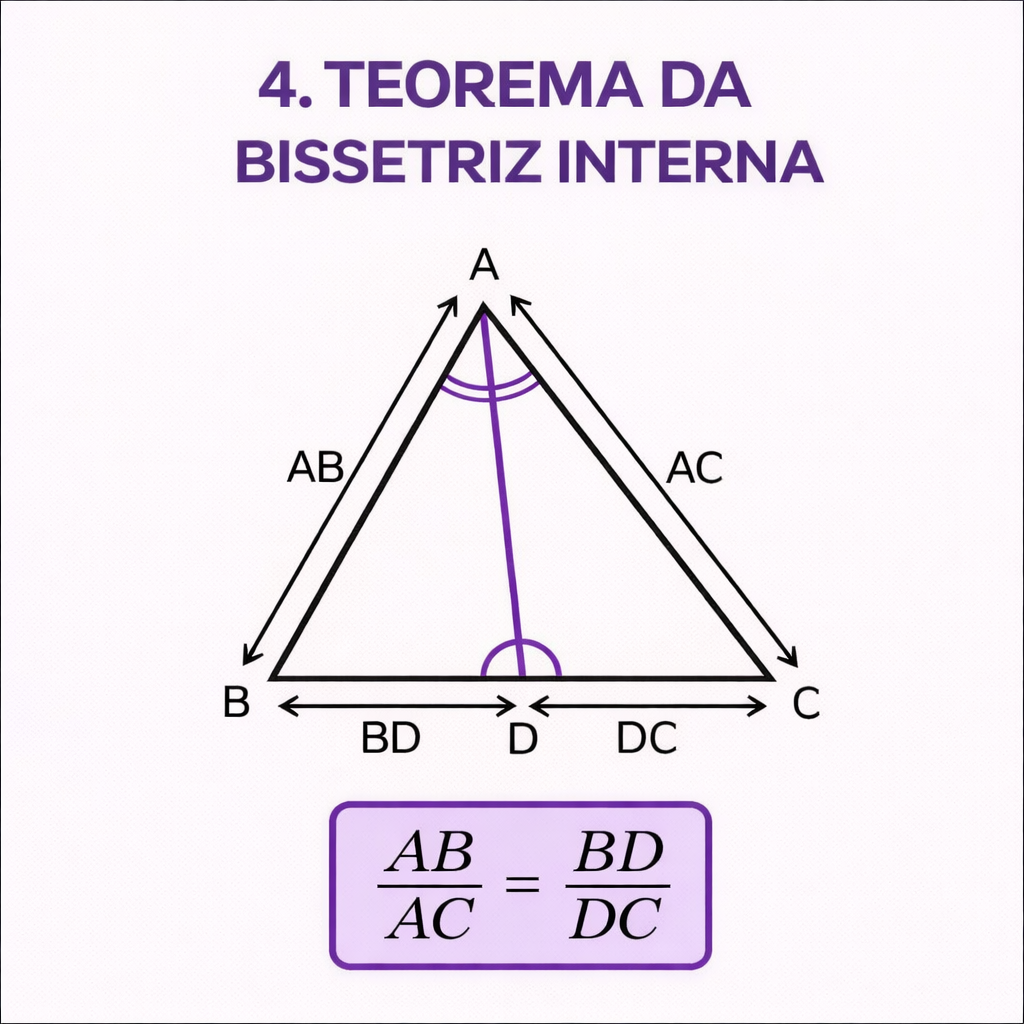
Na figura, temos o triângulo \(ABC\), em que o segmento \(AD\) é a bissetriz interna do ângulo em \(A\). O ponto \(D\) pertence ao lado \(BC\), dividindo-o em dois segmentos: \(BD\) e \(DC\).
Enunciado e fórmula do Teorema da Bissetriz Interna
O teorema pode ser enunciado assim:
Num triângulo \(ABC\), se a bissetriz interna do ângulo em \(A\) encontra o lado \(BC\) no ponto \(D\), então:
\(\displaystyle \frac{AB}{AC} = \frac{BD}{DC}\)
Ou seja, a bissetriz interna divide o lado oposto em segmentos proporcionais aos lados adjacentes ao ângulo.
Note que a razão entre os lados \(AB\) e \(AC\) é igual à razão entre os segmentos em que o lado oposto \(BC\) foi dividido, \(BD\) e \(DC\).
Intuição geométrica
Quando traçamos a bissetriz interna do ângulo em \(A\), dividimos o triângulo \(ABC\) em dois triângulos menores, \(ABD\) e \(ADC\). Esses triângulos compartilham a altura relativa ao lado \(BC\) e “herdam” a proporção dos lados \(AB\) e \(AC\).
De forma intuitiva, quanto maior for o lado \(AB\), maior será o segmento correspondente \(BD\); quanto maior for o lado \(AC\), maior será o segmento correspondente \(DC\). Daí surge a proporcionalidade:
\(\displaystyle \frac{AB}{AC} = \frac{BD}{DC}\).
Exemplo resolvido
Problema: No triângulo \(ABC\), o segmento \(AD\) é bissetriz interna do ângulo em \(A\). Sabemos que \(AB = 6\) cm, \(AC = 9\) cm e \(BD = 4\) cm. Determine o valor de \(DC\).
Usamos a relação do Teorema da Bissetriz Interna:
\(\displaystyle \frac{AB}{AC} = \frac{BD}{DC}\)
Substituindo os valores:
\(\displaystyle \frac{6}{9} = \frac{4}{DC}\)
Simplificamos a fração do lado esquerdo:
\(\displaystyle \frac{2}{3} = \frac{4}{DC}\)
Aplicando o produto em cruz:
\(2 \cdot DC = 3 \cdot 4 \Rightarrow 2\,DC = 12\)
Isolando \(DC\):
\(DC = \dfrac{12}{2} = 6\)
Resposta: \(DC = 6\) cm.
Exercícios para praticar
- No triângulo \(ABC\), \(AD\) é bissetriz interna. Sabendo que \(AB = 5\) cm, \(AC = 10\) cm e \(DC = 9\) cm, determine o valor de \(BD\).
- Em um triângulo, a bissetriz interna do ângulo em \(A\) divide o lado oposto em segmentos de 3 cm e 7 cm. Se \(AC = 14\) cm, qual é a medida de \(AB\)?
- Explique, em suas palavras, por que a bissetriz interna “favorece” mais o lado maior, produzindo um segmento oposto também maior.
Dica: em cada item, comece escrevendo a razão \(\dfrac{AB}{AC} = \dfrac{BD}{DC}\) e depois substitua os valores para montar uma equação simples.
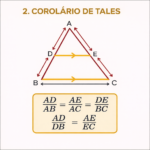
Relação com o Teorema de Tales e seus corolários
O Teorema da Bissetriz Interna pode ser demonstrado usando triângulos semelhantes, que por sua vez podem ser obtidos com o Teorema de Tales. Em muitos livros, a demonstração passa por construir paralelas ao lado \(BC\) e aplicar Tales para mostrar a proporção entre os segmentos.
Por isso, é interessante estudar este teorema junto com:
Esses quatro resultados formam um bloco muito explorado em provas, especialmente em questões de Geometria Plana com triângulos.
Aprofunde sua Geometria para ENEM e concursos
Use este teorema em conjunto com materiais completos do Matemática Hoje para acelerar seus resultados:
- Resolva questões do ENEM em ENEM Matemática — Questões Comentadas
- Baixe os 10 eBooks de Matemática para revisão completa
- Veja o Curso Matemática Básica: Do Zero à Confiança Prática
Continue estudando no Matemática Hoje
- Mapas Mentais de Matemática
- FGV 2025 – Matemática para Concurso
- Entre no grupo gratuito de Matemática no WhatsApp para receber questões, resumos e avisos de novos conteúdos.