Triângulo Inscrito (Triângulo Cíclico)
Panorama geral: Tipos de triângulos. Versão com foco em circunferências e incírculo: Triângulo inscrito na circunferência.
Definição
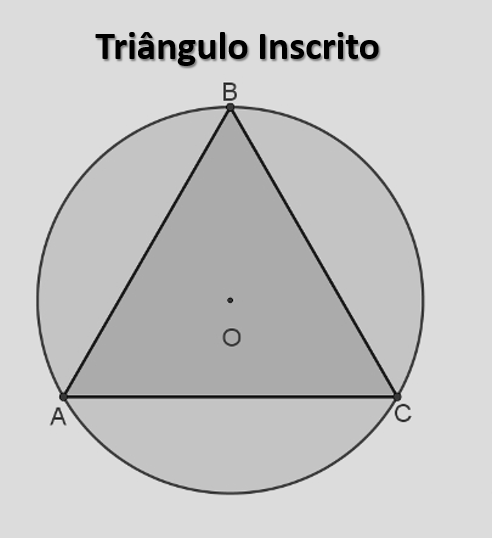
Um triângulo inscrito (ou triângulo cíclico) é aquele em que os três vértices estão sobre uma mesma circunferência, chamada circunferência circunscrita. O ponto de encontro das mediatrizes dos lados é o circuncentro \(O\) e sua distância aos vértices é o raio \(R\).
- Posição de \(O\): interna no acutângulo; no ponto médio da hipotenusa no retângulo; externa no obtusângulo. Consulte: acutângulo, retângulo, obtusângulo.
- Ângulos: ângulos inscritos que subtendem o mesmo arco são congruentes; um ângulo inscrito mede metade do ângulo central correspondente.
- Diâmetro como lado: se um lado do triângulo é diâmetro, o ângulo oposto é reto (Teorema de Tales).
Fórmulas essenciais (uma por linha)
Classificação por lados: equilátero, isósceles, escaleno. Técnicas de área: Área de triângulo. Centros: Pontos notáveis.
Exemplos resolvidos (passo a passo vertical)
Exemplo 1 — Em um triângulo inscrito, \(a=12\) e \(A=40^\circ\). Calcule \(R\).
Mostrar solução
\(R=\dfrac{a}{2\sin A}\)
\(=\dfrac{12}{2\sin 40^\circ}\)
\(=\dfrac{12}{2\cdot 0{,}6428}\)
\(=\dfrac{12}{1{,}2856}\)
\(\approx 9{,}34\).
Exemplo 2 — Para \(a=7\), \(b=8\), \(c=9\), determine \(R\).
Mostrar solução
\(s=\dfrac{7+8+9}{2}=12\)
\(A=\sqrt{12(12-7)(12-8)(12-9)}\)
\(=\sqrt{12\cdot 5\cdot 4\cdot 3}\)
\(=12\sqrt{5}\)\(\;\approx 26{,}833\)
\(R=\dfrac{abc}{4A}\)
\(=\dfrac{7\cdot 8\cdot 9}{4\cdot 12\sqrt5}\)
\(=\dfrac{504}{48\sqrt5}\)
\(=\dfrac{10{,}5}{\sqrt5}\approx 4{,}69\).
Exemplo 3 — Se \(A=90^\circ\) em um triângulo inscrito, relacione \(a\) e \(R\).
Mostrar solução
A hipotenusa coincide com o diâmetro da circunferência.
\(a=2R\).
Exercícios de múltipla escolha (com solução em abre/fecha)
1) Em triângulo inscrito, \(a=14\) e \(A=30^\circ\). O raio \(R\) é:
Mostrar solução
\(2R=\dfrac{a}{\sin A}=\dfrac{14}{\tfrac12}=28\Rightarrow R=14\).
2) Se \(R=10\) e \(A=\arcsin(0{,}6)\), então \(a\) vale:
Mostrar solução
\(a=2R\sin A=2\cdot 10\cdot 0{,}6=12\).
3) Em um triângulo inscrito, ângulos que subtendem o mesmo arco são:
Mostrar solução
Ângulos inscritos sobre o mesmo arco são iguais ⇒ congruentes.
4) Para \(a=6\), \(b=7\), \(c=8\) e \(R= \dfrac{abc}{4A}\), então a área \(A\) é:
Mostrar solução
Todas são expressões corretas para \(A\). Alternativa D.
5) Se \(A=90^\circ\) em triângulo inscrito, então:
Mostrar solução
Hipotenusa = diâmetro ⇒ \(a=2R\). Alternativa C.
6) Num triângulo equilátero de lado \(a\), o raio da circunferência circunscrita é:
Mostrar solução
\(a=2R\sin 60^\circ \Rightarrow R=a/\sqrt3\). Alternativa C. Veja triângulo equilátero.
7) Os lados de um triângulo são \(8, 15, 17\). O valor de \(R\) é:
Mostrar solução
Triângulo retângulo (\(8^2+15^2=17^2\)). Hipotenusa \(=17=2R\Rightarrow R=8{,}5\).
8) Se \(R=7\) e \(B=45^\circ\), então \(b\) é:
Mostrar solução
\(b=2R\sin B=14\cdot \frac{\sqrt2}{2}=7\sqrt2\). Alternativa D.
9) Para \(a=9\), \(b=10\), \(c=11\), calcule \(R\) (aprox.).
Mostrar solução
\(s=\dfrac{9+10+11}{2}=15\)
\(A=\sqrt{15\cdot 6\cdot 5\cdot 4}=\sqrt{1800}=42{,}426…\)
\(R=\dfrac{abc}{4A}=\dfrac{990}{4\cdot 42{,}426}\approx 5{,}83\)
Opção mais próxima: C) 6,0.
10) Qual afirmação está correta?
Mostrar solução
Lei dos Senos estendida: \(a=2R\sin A \Rightarrow \dfrac{a}{\sin A}=2R\). Correta: B.
Continue estudando
Triângulo inscrito na circunferência Triângulo retângulo Triângulo acutângulo Triângulo obtusângulo Triângulo equilátero Triângulo isósceles Triângulo escaleno Área de triângulo Pontos notáveis
Materiais recomendados
Mapas Mentais de Matemática
Resumo visual de cíclicos: \(a=2R\sin A\), \(A=\dfrac{abc}{4R}\) e muito mais.
Quero os Mapas+600 Questões ENEM Matemática
Geometria plana, semelhança e trigonometria com gabarito comentado.
Praticar agoraColeção 10 eBooks
Teoria objetiva + listas de exercícios resolvidos.
Ver coleçãoBanco de Questões
Monte suas listas por assunto e nível — perfeito para treino de triângulos cíclicos.
Acessar bancoCanais Oficiais
Receba novos artigos, listas e simulados no seu celular.
Entrar nos canais





















