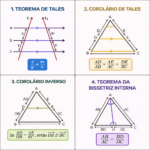
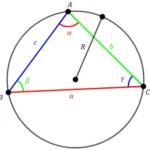
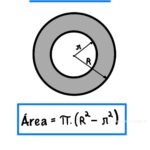
Triângulos Semelhantes — critérios, razão de semelhança, propriedades e exercícios

Triângulos semelhantes têm os ângulos correspondentes congruentes e os lados correspondentes proporcionais.

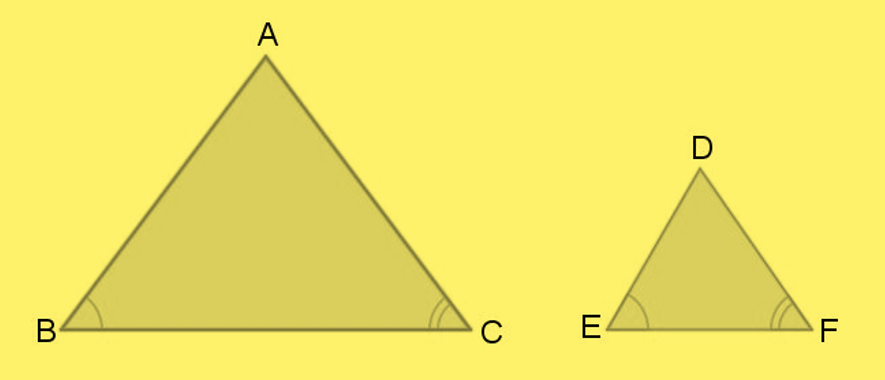
O que são triângulos semelhantes?

Dois triângulos são semelhantes quando seus ângulos correspondentes são iguais e seus lados correspondentes são proporcionais. Se os triângulos \(ABC\) e \(A’B’C’\) são semelhantes, escrevemos \( \triangle ABC \sim \triangle A’B’C’ \) e existe um número \(k>0\) (razão de semelhança) tal que:

Ângulos: \( \angle A=\angle A’,\; \angle B=\angle B’,\; \angle C=\angle C’ \). Lados: \( \displaystyle \frac{AB}{A’B’}=\frac{BC}{B’C’}=\frac{CA}{C’A’}=k \).

Para contextualizar, veja os tipos de triângulos e como a semelhança aparece em triângulo retângulo (por exemplo, com a altura na hipotenusa). Para revisão rápida, experimente os Mapas Mentais de Matemática.

Critérios de semelhança (como provar que dois triângulos são semelhantes)

AA (Ângulo-Ângulo): se dois ângulos de um são congruentes a dois ângulos do outro, então os triângulos são semelhantes.
LAL (Lado-Ângulo-Lado): se dois lados estão em proporção e o ângulo compreendido entre eles é congruente, os triângulos são semelhantes.
LLL (Lado-Lado-Lado): se os três pares de lados correspondentes estão em proporção, os triângulos são semelhantes.

Em triângulo equilátero e triângulo escaleno, a semelhança depende da comparação de ângulos e de razões entre lados. Para aplicações de área, veja Área de triângulo.

Razão de semelhança \(k\) e grandezas proporcionais

Lados correspondentes: \( \displaystyle \frac{AB}{A’B’}=\frac{BC}{B’C’}=\frac{CA}{C’A’}=k \). Perímetros: \( \displaystyle \frac{P}{P’}=k \). Áreas: \( \displaystyle \frac{A}{A’}=k^2 \). Alturas, medianas e bissetrizes correspondentes: proporcionais a \(k\).

Em triângulos retângulos, a altura à hipotenusa cria três triângulos semelhantes entre si, o que acelera cálculos de catetos, projeções e área. Para listas de prática editáveis, consulte o Banco de Questões.

Exemplos resolvidos (passo a passo vertical)

Exemplo 1 — Em \( \triangle ABC \sim \triangle A’B’C’ \), sabe-se que \(AB=9\), \(BC=12\), \(A’B’=6\). Calcule \(k\), \(B’C’\) e compare áreas.

Mostrar solução

\(k=\dfrac{AB}{A’B’}\)
\(=\dfrac{9}{6}\)
\(=\dfrac{3}{2}\).

\(\dfrac{BC}{B’C’}=k\Rightarrow B’C’=\dfrac{BC}{k}\)
\(=\dfrac{12}{3/2}\)
\(=12\cdot \dfrac{2}{3}\)
\(=8\).

\(\dfrac{A}{A’}=k^2=\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}\).

Para revisar antes da prova, use os Mapas Mentais.

Exemplo 2 — Dois triângulos têm lados correspondentes \(5,7,9\) e \(10,14,18\). Prove a semelhança e ache \(k\).

Mostrar solução

\(\dfrac{10}{5}=2,\; \dfrac{14}{7}=2,\; \dfrac{18}{9}=2\)
\(\Rightarrow\) três razões iguais
\(\Rightarrow\) critério LLL
\(\Rightarrow \triangle \sim \triangle\) com \(k=2\).

Logo, perímetros estão em razão \(2\) e áreas em \(2^2=4\).

Para consolidar com triângulos retângulos, veja este resumo.

Exercícios de múltipla escolha (com solução em abre/fecha)

1) Em triângulos semelhantes, \( \dfrac{AB}{A’B’}=\dfrac{BC}{B’C’}=\dfrac{CA}{C’A’}= \dfrac{3}{2} \). A razão entre as áreas é:

A) \( \dfrac{3}{2} \) B) \( \dfrac{9}{4} \) C) \( \dfrac{4}{9} \) D) \( \dfrac{2}{3} \) E) \( \dfrac{27}{8} \)

Mostrar solução

\(\dfrac{A}{A’}=k^2=\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}\).

Alternativa B.

2) Dois triângulos são semelhantes com \(k= \dfrac{5}{4}\) (lado do triângulo 1 sobre o correspondente do triângulo 2). Se \(P_2=48\), então \(P_1=\):

A) 45 B) 50 C) 54 D) 60 E) 64

Mostrar solução

\(\dfrac{P_1}{P_2}=k\)
\(P_1=\dfrac{5}{4}\cdot 48\)
\(=60\).

Alternativa D.

3) Em \( \triangle ABC \sim \triangle A’B’C’ \), \(AB=12\), \(A’B’=9\), \(B’C’=15\). O valor de \(BC\) é:

A) 18 B) 19 C) 20 D) 21 E) 22

Mostrar solução

\(k=\dfrac{AB}{A’B’}=\dfrac{12}{9}=\dfrac{4}{3}\).

\(\dfrac{BC}{B’C’}=k \Rightarrow BC=k\cdot B’C’\)
\(=\dfrac{4}{3}\cdot 15\)
\(=20\).

Alternativa C.

4) Se triângulos são semelhantes e uma altura de um corresponde a uma altura de outro, a razão entre essas alturas é:

A) \(k\) B) \(k^2\) C) \(1/k\) D) \(k^3\) E) \(k/2\)

Mostrar solução

Alturas correspondentes \(\propto k\). Alternativa A.

5) Considere \(k=\dfrac{\text{menor}}{\text{maior}}=\dfrac{2}{3}\). Se a área do triângulo maior é \(A_{\text{maior}}=72\), então a área do menor é:

A) 32 B) 40 C) 48 D) 54 E) 81

Mostrar solução

\(\dfrac{A_{\text{menor}}}{A_{\text{maior}}}=k^2=\left(\dfrac{2}{3}\right)^2=\dfrac{4}{9}\).

\(A_{\text{menor}}=\dfrac{4}{9}\cdot 72\)
\(=32\).

Alternativa A.

6) Lados correspondentes \(7,9,11\) e \(14,18,22\). O critério que garante semelhança é:

A) AA B) LAL C) LLL D) SSA E) ALA

Mostrar solução

\(\dfrac{14}{7}=2,\; \dfrac{18}{9}=2,\; \dfrac{22}{11}=2\)
\(\Rightarrow\) três razões iguais \(\Rightarrow\) LLL.

Alternativa C.

7) Em dois triângulos, \(AB=10\), \(A’B’=15\); \(AC=14\), \(A’C’=21\); e o ângulo compreendido é igual. O critério é:

A) AA B) LAL C) LLL D) AAS E) SAS

Mostrar solução

\(\dfrac{AB}{A’B’}=\dfrac{10}{15}=\dfrac{2}{3},\quad \dfrac{AC}{A’C’}=\dfrac{14}{21}=\dfrac{2}{3}\)
Ângulo compreendido igual \(\Rightarrow\) **LAL**.

Alternativa B.

8) Considere \(k=\dfrac{\text{menor}}{\text{maior}}=\dfrac{3}{4}\). Se a mediana do triângulo maior mede \(12\), a mediana correspondente do menor mede:

A) 8 B) 9 C) 10 D) 12 E) 16

Mostrar solução

\(\dfrac{m_{\text{menor}}}{m_{\text{maior}}}=k=\dfrac{3}{4}\)
\(m_{\text{menor}}=\dfrac{3}{4}\cdot 12\)
\(=9\).

Alternativa B.

9) \(k=\dfrac{\text{maior}}{\text{menor}}=\dfrac{5}{3}\). Se \(P_{\text{maior}}=40\), então \(P_{\text{menor}}\) é:

A) 20 B) 22 C) 24 D) 26 E) 30

Mostrar solução

\(\dfrac{P_{\text{maior}}}{P_{\text{menor}}}=k\Rightarrow P_{\text{menor}}=\dfrac{P_{\text{maior}}}{k}\)
\(=\dfrac{40}{5/3}\)
\(=40\cdot \dfrac{3}{5}\)
\(=24\).

Alternativa C.

10) \(k=\dfrac{\text{maior}}{\text{menor}}=\dfrac{4}{3}\). Se \(A_{\text{menor}}=18\), a área do maior é:

A) 24 B) 28 C) 30 D) 32 E) 40

Mostrar solução

\(\dfrac{A_{\text{maior}}}{A_{\text{menor}}}=k^2=\left(\dfrac{4}{3}\right)^2=\dfrac{16}{9}\)
\(A_{\text{maior}}=\dfrac{16}{9}\cdot 18\)
\(=32\).

Alternativa D.

Quer listas maiores com gabarito editável? Veja o Banco de Questões e o pacote ENEM Matemática.

Relações importantes e estudos recomendados

Triângulo retângulo Área de triângulo Pontos notáveis Tipos de triângulos Triângulo equilátero Triângulo escaleno

Para revisão rápida com quadros-resumo e mapas de fórmulas (razão \(k\), áreas, perímetros), use os Mapas Mentais de Matemática. Eles aceleram sua preparação para provas.