UNICAMP 2021 – Questão de Geometria Analítica
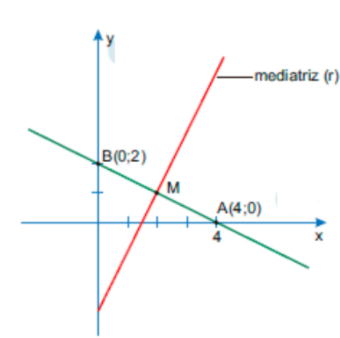
No plano cartesiano, considere a reta de equação \( x + 2y = 4 \), sendo \( A, B \) os pontos de interseção dessa reta com os eixos coordenados.
A equação da reta **mediatriz** do segmento de reta \( AB \) é dada por:
a) \( 2x – y = 3 \)
b) \( 2x – y = 5 \)
c) \( 2x + y = 3 \)
d) \( 2x – y = 5 \)
a) \( 2x – y = 3 \)
b) \( 2x – y = 5 \)
c) \( 2x + y = 3 \)
d) \( 2x – y = 5 \)
- Primeiro, determinamos o **ponto médio** \( M \) de \( AB \): \[ A(4,0), \quad B(0,2) \] \[ M = \left( \frac{4+0}{2}, \frac{0+2}{2} \right) = (2,1) \]
- Calculamos a **inclinação** da reta \( AB \): \[ m_{AB} = \frac{0-2}{4-0} = -\frac{1}{2} \] A mediatriz é perpendicular, logo: \[ m_r = 2 \]
- Equação da mediatriz passando por \( M(2,1) \): \[ y-1 = 2(x-2) \] \[ 2x – y = 3 \]
- Portanto, a resposta correta é **A**.
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:













