UNICAMP 2022 | Matemática | Vacinação e Epidemia
Para conter uma epidemia viral, uma vacina será aplicada a uma população. Sabe-se que:
- A efetividade de uma vacina pode ser entendida como a porcentagem de indivíduos vacinados que estarão imunes à doença;
- Para controlar a epidemia, a porcentagem mínima de uma população a ser imunizada é dada por: \[ I(R_0) = 100 \frac{(R_0 – 1)}{R_0}, \quad R_0 > 1 \]
Assume-se que a imunização ocorre apenas pela vacina. Em relação à epidemia e à vacinação, é correto afirmar que:
a) A porcentagem mínima da população a ser vacinada para controlar a epidemia é sempre maior que 50%.
b) Para uma vacina, quanto maior \( R_0 \), menor a porcentagem mínima da população que deve ser vacinada.
c) Para uma vacina, quanto maior \( R_0 \), maior a porcentagem mínima da população que deve ser vacinada para controlar a epidemia.
d) Para um dado \( R_0 \), quanto maior a efetividade da vacina, maior a porcentagem mínima da população a ser vacinada.
Resolução:
A função que indica a porcentagem mínima é: \[ I(R_0) = 100 \cdot \frac{R_0 – 1}{R_0} = 100 \left(1 – \frac{1}{R_0}\right) \]
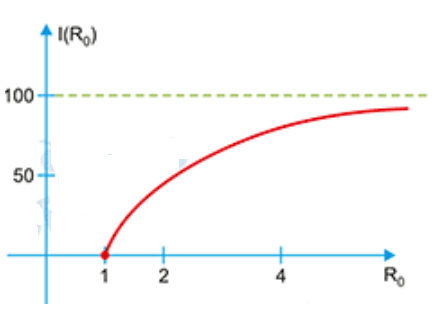
Como \( R_0 > 1 \), temos que \( I(R_0) \) é uma função crescente, portanto, quanto maior \( R_0 \), maior será a porcentagem mínima da população que precisa ser vacinada.
Resposta: c) Para uma vacina, quanto maior \( R_0 \), maior a porcentagem mínima da população a ser vacinada.📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:




























