Como converter unidades de comprimento corretamente?
Converter entre quilômetro (km), hectômetro (hm), decâmetro (dam), metro (m), decímetro (dm), centímetro (cm) e milímetro (mm) é rotina em problemas escolares, provas e situações do dia a dia. Neste guia visual e direto ao ponto você verá a escada de conversão, regras práticas, exemplos resolvidos com todos os passos em linhas separadas e uma lista de exercícios com gabarito em “abre/fecha”.
Resumo visual das principais fórmulas de conversão, geometria, álgebra e muito mais. Ideal para revisões rápidas.
Quero meu eBook gratuitoEntendendo a escala métrica e a lógica da “escada”
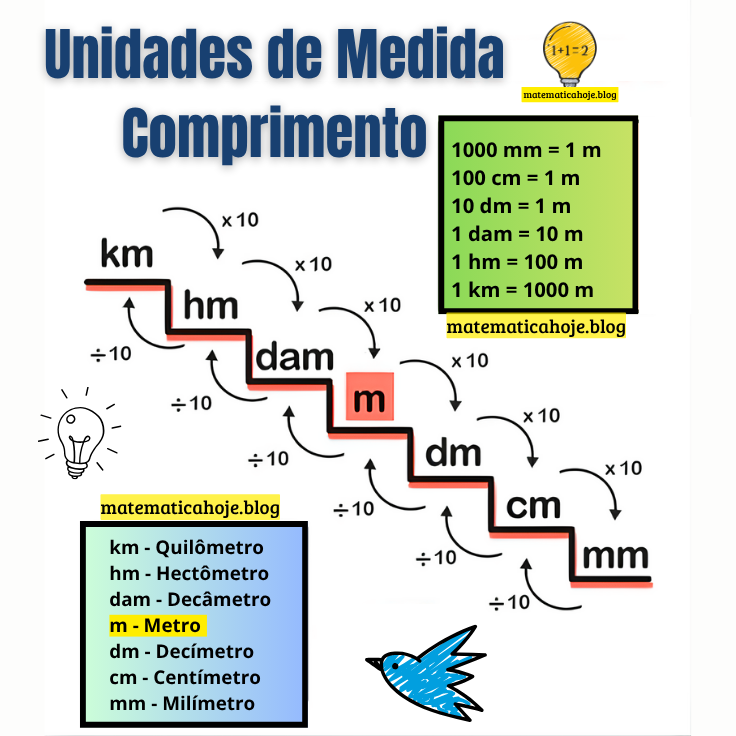
O Sistema Internacional organiza as unidades em potências de 10. Por isso, cada passo entre unidades vizinhas representa um fator ×10 (descendo) ou ÷10 (subindo). Assim, \(1\,\text{km}=1000\,\text{m}\), \(1\,\text{m}=100\,\text{cm}\) e \(1\,\text{cm}=10\,\text{mm}\).
| Unidade | Símbolo | Relação com o metro | Equivalência |
|---|---|---|---|
| Quilômetro | km | \(10^3\) | 1 km = 1000 m |
| Hectômetro | hm | \(10^2\) | 1 hm = 100 m |
| Decâmetro | dam | \(10^1\) | 1 dam = 10 m |
| Metro | m | \(10^0\) | Unidade base |
| Decímetro | dm | \(10^{-1}\) | 1 m = 10 dm |
| Centímetro | cm | \(10^{-2}\) | 1 m = 100 cm |
| Milímetro | mm | \(10^{-3}\) | 1 m = 1000 mm |
Como fazer conversões entre unidades de comprimento
Transformando medidas maiores em menores (multiplicar por 10)
Descendo a escada (km → m → cm → mm) aumentamos o número multiplicando por potências de 10.
\(2{,}5\,\text{km} = 2{,}5 \times 1000\,\text{m}\)
\(= 2500\,\text{m}\)
Transformando medidas menores em maiores (dividir por 10)
Subindo a escada (mm → cm → m → km) reduzimos o número dividindo por potências de 10.
\(850\,\text{mm} = 850 \div 1000\,\text{m}\)
\(= 0{,}85\,\text{m}\)
Conversões não adjacentes (use o total de degraus)
hm → m (×10) e m → cm (×100) ⇒ total ×1000.
\(3{,}2\,\text{hm} = 3{,}2 \times 1000\,\text{cm}\)
\(= 3200\,\text{cm}\)
Quer revisar medidas e conversões em minutos? Use mapas mentais prontos para impressão.
Ver Mapas MentaisConversões com notação científica
Exemplo 4 — Engenharia: \(7{,}5\times10^4\,\text{mm}\) em metros.
\(1\,\text{m}=10^3\,\text{mm}\Rightarrow\) dividir por \(10^3\).
\(7{,}5\times10^4\,\text{mm} = 7{,}5\times10^4 \div 10^3\,\text{m}\)
\(= 7{,}5\times10^1\,\text{m}=75\,\text{m}\)
Comparando comprimentos com unidades distintas
Exemplo 5 — Corrida: O que é maior, \(120\,\text{dm}\) ou \(11\,\text{m}\)?
\(120\,\text{dm}=12\,\text{m}\)
Logo, \(12\,\text{m} > 11\,\text{m}\).
Exemplos práticos do cotidiano (passo a passo)
\(30\,\text{cm} = 30 \times 10\,\text{mm}\)
\(= 300\,\text{mm}\).
km → hm: ÷10.
\(2{,}4\,\text{km} = 2{,}4 \div 10\,\text{hm}\)
\(= 0{,}24\,\text{hm}\).
\(1250 \div 1000 = 1{,}25\,\text{m}\).
Lista de exercícios com gabarito passo a passo
Exercício 1 — Trena: transforme \(4{,}6\,\text{m}\) para centímetros.
\(= 460\,\text{cm}\).
Exercício 2 — Jardim: converta \(780\,\text{cm}\) para metros.
\(= 7{,}8\,\text{m}\).
Exercício 3 — Construção: \(3{,}2\,\text{dam}\) em milímetros.
\(3{,}2\,\text{dam} = 3{,}2 \times 10000\,\text{mm}\)
\(= 32000\,\text{mm}\).
Exercício 4 — Atleta: compare \(150\,\text{dm}\) com \(14\,\text{m}\).
Como \(15\,\text{m} > 14\,\text{m}\), então \(150\,\text{dm} > 14\,\text{m}\).
Exercício 5 — Impressora 3D: \(0{,}045\,\text{m}\) para milímetros.
\(= 45\,\text{mm}\).
Exercício 6 — Estrada: \(1{,}2\times10^3\,\text{m}\) para quilômetros.
\(1200\,\text{m} \div 1000 = 1{,}2\,\text{km}\).
Links úteis para continuar estudando
Tenha à mão um resumo das fórmulas que mais caem em provas, incluindo conversões de unidades, geometria e porcentagem.
Baixar agoraConclusão: dominando conversões com confiança
A “escada” de unidades resolve quase todos os problemas de comprimento: contar degraus e multiplicar ou dividir por 10 é o caminho mais rápido. Para treinar, resolva os exercícios deste artigo, use nossos mapas mentais e mantenha o eBook de fórmulas como atalho de revisão. Com prática, as conversões entre km, m, cm e mm tornam-se automáticas.
Perguntas frequentes (FAQ)
Como lembrar se devo multiplicar ou dividir nas conversões?
Descendo a escada (de unidades maiores para menores) multiplica por 10 a cada degrau; subindo, divide por 10. Visualize a ordem km → … → mm para não errar.
Qual é o jeito mais rápido em provas do ENEM ou concursos?
Converta tudo para a mesma unidade antes de comparar ou somar. Em geral, meter para centímetros ou metros facilita contas e evita erros comuns.
Quando usar notação científica nas medidas?
Use quando os números forem muito grandes ou pequenos. A notação científica organiza as potências de 10 e reduz o risco de perder zeros em contas.
Posso pular unidades intermediárias numa conversão?
Sim. Conte quantos degraus há entre a unidade de origem e a de destino, depois aplique \(10^n\) (multiplicando ou dividindo) de uma vez só.
Qual a diferença entre comprimento, área e volume nas conversões?
Comprimento muda em potências de 10. Para área, os fatores são \(10^2\); para volume, \(10^3\). Não confunda: m, m² e m³ têm escalas distintas.