Neste artigo vamos revisar, de forma bem didática, as principais fórmulas de áreas de figuras planas que aparecem em provas, concursos e no ENEM. A ideia é que você consiga olhar para cada fórmula, entender de onde ela vem intuitivamente e, logo em seguida, aplicar em uma situação-problema simples.
Se quiser ter todas essas fórmulas organizadas em um material de revisão rápida, vale a pena conferir o eBook gratuito de Fórmulas de Matemática , que complementa muito bem este estudo.
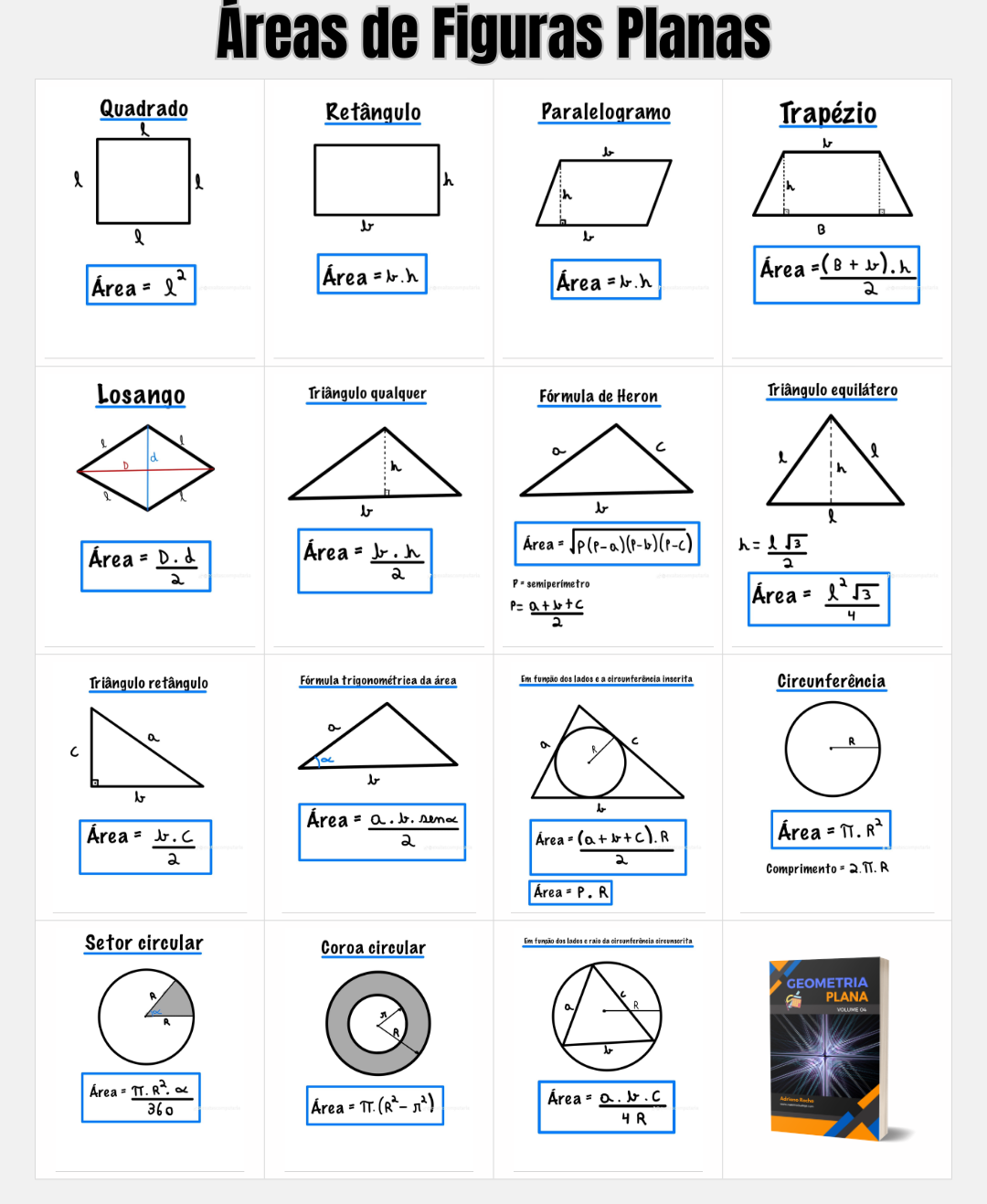
Ao longo do texto, cada figura virá com um resumo da ideia principal, a fórmula destacada em azul claro e um exercício contextualizado, como se fosse aquele tipo de questão que o professor leva para a sala de aula.
1. Área do Quadrado
O quadrado é uma figura em que todos os lados são iguais. Quando multiplicamos um lado por ele mesmo, descobrimos quantas “unidades de área” cabem dentro da figura.
A professora pediu para João calcular a área de um piso quadrado que ele irá revestir em sua casa. O lado do piso mede 6 cm.
Qual é a área desse piso?
Resolução:
\( A = l^2 = 6^2 = 36 \,\text{cm}^2 \)
2. Área do Retângulo
No retângulo, os lados opostos são iguais, e a área é a multiplicação da base pela altura. É a mesma lógica de contar quantos quadradinhos cabem em um “tapete” retangular.
Um quadro retangular será colocado na parede da sala. Sua base mede 12 cm e sua altura 5 cm.
Qual a área ocupada pelo quadro?
Resolução:
\( A = b \cdot h = 12 \cdot 5 = 60 \,\text{cm}^2 \)
3. Área do Paralelogramo
No paralelogramo, a base e a altura funcionam como no retângulo. A altura é o segmento perpendicular à base, mesmo que a figura esteja “inclinada”.
Um terreno tem formato aproximado de um paralelogramo, com base de 10 m e altura de 7 m.
Qual é a área desse terreno?
Resolução:
\( A = 10 \cdot 7 = 70 \,\text{m}^2 \)
4. Área do Trapézio
O trapézio possui duas bases paralelas (uma maior e uma menor). A área é a média aritmética dessas bases multiplicada pela altura.
Uma piscina infantil tem formato de trapézio. As bases medem 14 m e 8 m, e a altura é de 5 m.
Qual é a área da superfície da água?
Resolução:
\( A = \dfrac{(14 + 8) \cdot 5}{2} = \dfrac{22 \cdot 5}{2} = 55 \,\text{m}^2 \)
5. Área do Losango
O losango tem quatro lados iguais e duas diagonais que se cruzam formando ângulos retos. A área é o produto das diagonais dividido por 2.
Uma placa de sinalização possui formato de losango, com diagonais medindo 10 cm e 6 cm.
Qual é a área dessa placa?
Resolução:
\( A = \dfrac{10 \cdot 6}{2} = 30 \,\text{cm}^2 \)
6. Área do Triângulo Qualquer
Em qualquer triângulo, se conhecemos uma base e a altura relativa a essa base, podemos calcular a área com a fórmula tradicional “base vezes altura dividido por 2”.
Uma peça metálica triangular tem base de 12 cm e altura de 4 cm.
Qual é a área dessa peça?
Resolução:
\( A = \dfrac{12 \cdot 4}{2} = 24 \,\text{cm}^2 \)
Organize seus estudos de Matemática com materiais práticos
Revise os principais conteúdos de forma visual e objetiva, com mapas mentais prontos para imprimir ou estudar pelo celular.
Acessar Mapas Mentais de MatemáticaQuestões comentadas, temas recorrentes e dicas para aumentar sua nota na prova de matemática do ENEM.
Acessar ENEM MatemáticaColeção completa para quem quer revisar conteúdos de matemática para concursos, ENEM e vestibulares.
Conhecer os 10 eBooksCentenas de exercícios organizados por assunto para você praticar exatamente o que cai nas provas.
Acessar o Banco de QuestõesTenha todas as principais fórmulas de matemática em um único PDF para consulta rápida durante os estudos e revisões.
Baixar eBook de Fórmulas (Grátis)7. Área do Triângulo pela Fórmula de Heron
Quando conhecemos apenas os três lados de um triângulo, sem a altura, a fórmula de Heron resolve o problema usando o semiperímetro \( p \).
Área: \( A = \sqrt{p(p-a)(p-b)(p-c)} \)
Um engenheiro precisa calcular a área de um triângulo cujos lados medem 5 m, 6 m e 7 m.
Qual é a área aproximada desse triângulo?
Resolução:
\( p = \dfrac{5 + 6 + 7}{2} = 9 \)
\( A = \sqrt{9 \cdot 4 \cdot 3 \cdot 2} = \sqrt{216} \approx 14{,}7 \,\text{m}^2 \)
8. Área do Triângulo Equilátero
No triângulo equilátero todos os lados são iguais e todos os ângulos internos medem 60°. A fórmula específica usa \( \sqrt{3} \) porque surge da geometria de um triângulo retângulo 30°–60°–90°.
Uma placa decorativa tem formato de triângulo equilátero com lado 8 cm.
Qual é a área dessa placa?
Resolução:
\( A = \dfrac{8^2 \sqrt{3}}{4} = 16 \sqrt{3} \approx 27{,}7 \,\text{cm}^2 \)
9. Área do Triângulo Retângulo
Em um triângulo retângulo, os dois catetos funcionam como base e altura. Por isso, a área é o produto dos catetos dividido por 2.
Um telhadista precisa calcular a área de uma parte do telhado em forma de triângulo retângulo, com catetos medindo 9 m e 12 m.
Qual é a área dessa região?
Resolução:
\( A = \dfrac{9 \cdot 12}{2} = 54 \,\text{m}^2 \)
10. Área do Triângulo pela Fórmula Trigonométrica
Quando conhecemos dois lados e o ângulo entre eles, podemos usar a trigonometria. Essa fórmula aparece muito em questões de geometria envolvendo lei dos senos e dos cossenos.
Um engenheiro mede dois lados de um triângulo de uma estrutura: \( a = 10 \) cm, \( b = 8 \) cm e o ângulo entre eles é de \( 30^\circ \).
Qual é a área aproximada da região triangular?
Resolução:
\( A = \dfrac{10 \cdot 8 \cdot \sin 30^\circ}{2} = \dfrac{80 \cdot 0{,}5}{2} = 20 \,\text{cm}^2 \)
11. Área do Triângulo em Função do Raio da Circunferência Circunscrita
Se um triângulo está inscrito em uma circunferência de raio \( R \), é possível relacionar a área com o produto dos lados e esse raio, usando a fórmula:
Um triângulo está inscrito em uma circunferência de raio 5 cm, e seus lados medem 6 cm, 7 cm e 8 cm.
Calcule a área desse triângulo.
Resolução:
\( A = \dfrac{6 \cdot 7 \cdot 8}{4 \cdot 5} = \dfrac{336}{20} = 16{,}8 \,\text{cm}^2 \)
12. Área do Triângulo em Função do Semiperímetro e do Raio da Inscrita
Todo triângulo possui uma circunferência inscrita (tangente aos três lados). Se chamarmos o semiperímetro de \( p \) e o raio dessa circunferência de \( r \), a área pode ser calculada por:
Um triângulo tem lados de 7 cm, 8 cm e 9 cm. O raio da circunferência inscrita mede 3 cm.
Qual é a área desse triângulo?
Resolução:
\( p = \dfrac{7 + 8 + 9}{2} = 12 \)
\( A = p \cdot r = 12 \cdot 3 = 36 \,\text{cm}^2 \)
13. Área do Círculo (Disco)
A área de um círculo é proporcional ao quadrado do raio. Quanto maior o raio, muito mais a área cresce, porque ele aparece ao quadrado na fórmula.
Uma mesa redonda possui raio de 5 cm.
Calcule a área aproximada do tampo dessa mesa.
Resolução:
\( A = \pi \cdot 5^2 = 25\pi \approx 78{,}5 \,\text{cm}^2 \)
14. Comprimento da Circunferência
O comprimento da circunferência é o “perímetro” do círculo, isto é, a distância ao redor da borda.
Um artesão quer colocar uma fita em volta de um disco de madeira de raio 4 cm.
Qual deve ser o comprimento mínimo da fita?
Resolução:
\( C = 2\pi \cdot 4 = 8\pi \,\text{cm} \)
15. Área do Setor Circular
O setor circular é “um pedaço da pizza”. A área é uma fração da área total do círculo, proporcional ao ângulo central \( \alpha \).
Em um gráfico de pizza, um setor de 90° representa a quantidade de votos de um candidato. O gráfico tem raio 6 cm.
Qual é a área desse setor?
Resolução:
\( A = \dfrac{\pi \cdot 6^2 \cdot 90}{360} = \dfrac{\pi \cdot 36 \cdot 90}{360} = 9\pi \,\text{cm}^2 \)
16. Área da Coroa Circular
A coroa circular é a região entre dois círculos concêntricos (mesmo centro). A área é a diferença entre as áreas dos dois discos.
Um alvo de tiro possui uma parte externa com raio 10 cm e uma região central circular de raio 6 cm.
Qual é a área apenas da faixa entre esses dois círculos?
Resolução:
\( A = \pi(10^2 – 6^2) = \pi(100 – 36) = 64\pi \,\text{cm}^2 \)
17. Outra Aplicação da Fórmula com Raio da Circunferência Circunscrita
Para fixar a ideia, vamos repetir o uso da fórmula \( \dfrac{abc}{4R} \) em um triângulo com outros valores de lados e raio.
Um triângulo possui lados de 5 cm, 6 cm e 7 cm, e está inscrito em uma circunferência de raio 4 cm.
Calcule a área desse triângulo.
Resolução:
\( A = \dfrac{5 \cdot 6 \cdot 7}{4 \cdot 4} = \dfrac{210}{16} = 13{,}125 \,\text{cm}^2 \)
Estudar áreas de figuras planas com situações reais ajuda a memorizar as fórmulas de forma muito mais natural. Sempre que possível, tente desenhar as figuras, marcar medidas, identificar base e altura e, depois, aplicar a fórmula destacada em azul. Essa rotina acelera bastante a aprendizagem e deixa você pronto para as questões mais cobradas em provas e concursos.
Organize seus estudos de Matemática com materiais práticos
Revise os principais conteúdos de forma visual e objetiva, com mapas mentais prontos para imprimir ou estudar pelo celular.
Acessar Mapas Mentais de MatemáticaQuestões comentadas, temas recorrentes e dicas para aumentar sua nota na prova de matemática do ENEM.
Acessar ENEM MatemáticaColeção completa para quem quer revisar conteúdos de matemática para concursos, ENEM e vestibulares.
Conhecer os 10 eBooksCentenas de exercícios organizados por assunto para você praticar exatamente o que cai nas provas.
Acessar o Banco de QuestõesTenha todas as principais fórmulas de matemática em um único PDF para consulta rápida durante os estudos e revisões.
Baixar eBook de Fórmulas (Grátis)