Contradomínio de uma Função
Definição, diferença para imagem, exemplos e exercícios resolvidos.
O contradomínio é um dos três pilares de funções ao lado de domínio e imagem. Em provas (ENEM e concursos) muitas questões exploram exatamente a distinção entre contradomínio e imagem.
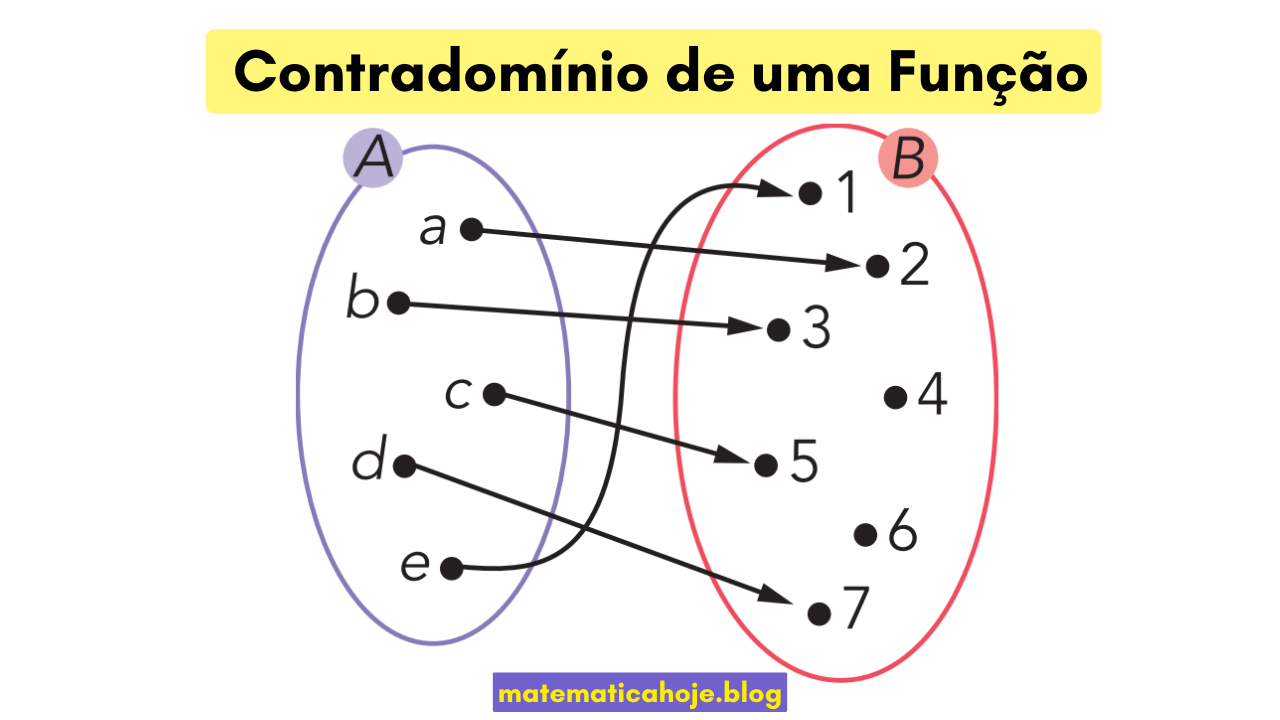
Contradomínio × Imagem
- Contradomínio \(B\): conjunto de “saídas possíveis” escolhido pelo enunciado.
- Imagem \(\mathrm{Im}(f)\): saídas efetivamente obtidas; sempre \(\mathrm{Im}(f)\subseteq B\).
- Se \(\mathrm{Im}(f)=B\), então \(f\) é sobrejetora (ou “sujeitora”).
Leituras relacionadas
Conjuntos Numéricos • Função do 2º Grau • Equações do 1º Grau • Banco de Questões
Como escolher o contradomínio?
- O contradomínio é declarado no enunciado. Ex.: “\(f:\mathbb{R}\to\mathbb{R}\)”, ou “\(f:\mathbb{Z}\to\mathbb{Z}\)”.
- Quando não for explícito, use o conjunto natural do problema (ex.: funções reais: \(A,B\subseteq\mathbb{R}\)).
- Trocar o contradomínio pode mudar a classificação da função (deixar de ser sobrejetora, por exemplo).
Exemplos comentados
Exemplo 1 — Mesmo \(f(x)=x^2\), contradomínios diferentes
| Definição | Contradomínio | Imagem | Sobrejetora? |
|---|---|---|---|
| \(f:\mathbb{R}\to\mathbb{R}\), \(f(x)=x^2\) | \(\mathbb{R}\) | \([0,\infty)\) | Não |
| \(g:\mathbb{R}\to[0,\infty)\), \(g(x)=x^2\) | \([0,\infty)\) | \([0,\infty)\) | Sim |
Exemplo 2 — Função afim
\(h:\mathbb{R}\to\mathbb{R}\), \(h(x)=2x-3\). Aqui \(\mathrm{Im}(h)=\mathbb{R}\). Como o contradomínio também é \(\mathbb{R}\), a função é sobrejetora e injetora (bijetora).
Exemplo 3 — Função exponencial
\(p:\mathbb{R}\to\mathbb{R}\), \(p(x)=2^x\). A imagem é \((0,\infty)\). Com contradomínio \(\mathbb{R}\), não é sobrejetora. Se definimos \(p:\mathbb{R}\to(0,\infty)\), passa a ser sobrejetora.
Praticar questões de FunçõesExercícios (múltipla escolha) com solução
1) Considere \(f:\mathbb{R}\to\mathbb{R}\) com \(f(x)=x^2+1\). O contradomínio é:
- \([1,\infty)\)
- \(\mathbb{R}\)
- \((0,\infty)\)
- \([0,\infty)\)
Ver solução
2) Seja \(g:\mathbb{R}\to[0,\infty)\) definido por \(g(x)=x^2\). Classifique quanto à sobrejetividade.
- Não é sobrejetora.
- É sobrejetora.
- Não é definida.
- É sobrejetora apenas em \(x\ge0\).
Ver solução
3) Para \(h:\mathbb{R}\to\mathbb{R}\) com \(h(x)=e^x\), assinale a alternativa correta.
- \(\mathrm{Im}(h)=\mathbb{R}\) e é sobrejetora.
- \(\mathrm{Im}(h)=(0,\infty)\) e não é sobrejetora em \(\mathbb{R}\).
- \(\mathrm{Im}(h)=(0,\infty)\) e é sobrejetora em \(\mathbb{R}\).
- \(\mathrm{Im}(h)=\mathbb{R}\setminus\{0\}\) e é sobrejetora.
Ver solução
4) A função \(p:\mathbb{Z}\to\mathbb{Z}\), \(p(x)=2x\), é sobrejetora?
- Sim, pois atinge qualquer inteiro.
- Não, pois só atinge os inteiros pares.
- Sim, pois \(2x\) cresce sem limites.
- Depende do domínio.
Ver solução
5) Reescreva \(q\) para torná-la sobrejetora: \(q:\mathbb{R}\to\mathbb{R}\), \(q(x)=|x|\).
- Trocar para \(q:\mathbb{R}\to[0,\infty)\).
- Trocar para \(q:(0,\infty)\to\mathbb{R}\).
- Trocar para \(q:[0,\infty)\to\mathbb{R}\).
- Não é possível.
Ver solução
6) Dada \(r:\mathbb{R}\to(0,\infty)\) com \(r(x)=\ln(x^2+1)+2\), qual é a relação entre imagem e contradomínio?
- A imagem é \((-\infty,\infty)\), igual ao contradomínio.
- A imagem é \([2,\infty)\), subconjunto próprio do contradomínio.
- A imagem é \((0,\infty)\), igual ao contradomínio.
- A imagem é \((-\infty,2]\), subconjunto do contradomínio.
Ver solução
Continue estudando
- Domínio de uma Função
- Imagem de uma Função
- Coleção 10 eBooks de Matemática
- Banco de Questões Matemática