21. Durante a aula de Matemática, o professor comentou sobre uma função que representava o crescimento de uma população de bactérias e escreveu na lousa \( f(t) = 2^t \), para \( t \geq 0 \), em que \( t \) é dado em horas e \( f(t) \) em milhares de bactérias.
Um estudante distraído copiou \( f(t) = 2t \) e, portanto, seus cálculos não deram certo.
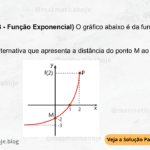
- Esboce os gráficos das duas funções em um mesmo sistema de coordenadas.
- Observando os gráficos construídos no item a, existe algum valor de \( t \) para o qual as duas funções assumem valor igual? Se sim, qual(is)?
- O que você pode concluir sobre o crescimento dessas duas funções?
- Para \( t = 3 \) h, qual é a diferença entre o número de bactérias nas duas funções?
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Duas funções foram dadas:
- Função correta: \( f(t) = 2^t \) – exponencial (crescimento acelerado)
- Função copiada: \( f(t) = 2t \) – linear (crescimento constante)
a) Esboço dos gráficos:
Ambas começam em \( f(0) = 1 \), mas a função exponencial cresce mais rapidamente com o tempo. No gráfico:
- \( 2^0 = 1 \), \( 2^1 = 2 \), \( 2^2 = 4 \), \( 2^3 = 8 \), …
- \( 2 \cdot 0 = 0 \), \( 2 \cdot 1 = 2 \), \( 2 \cdot 2 = 4 \), \( 2 \cdot 3 = 6 \), …
b) Valores iguais:
As funções coincidem quando seus valores são iguais:
- Para \( t = 1 \): \( 2^1 = 2 \) e \( 2 \cdot 1 = 2 \)
- Para \( t = 2 \): \( 2^2 = 4 \) e \( 2 \cdot 2 = 4 \)
Resposta: Sim, para \( t = 1 \) e \( t = 2 \)
c) Conclusão sobre o crescimento:
Ambas as funções são crescentes, porém:
- A função linear cresce de forma constante.
- A função exponencial cresce mais rapidamente à medida que o tempo aumenta.
Conclusão: Ambas são crescentes, mas a exponencial cresce mais rápido.
d) Diferença para \( t = 3 \):
– \( f_{\text{exponencial}}(3) = 2^3 = 8 \) (milhares de bactérias)
– \( f_{\text{linear}}(3) = 2 \cdot 3 = 6 \) (milhares de bactérias)
– Diferença: \( 8 – 6 = 2 \) mil = 2000 bactérias
✅ Resumo final:
- b) Sim, valores iguais para \( t = 1 \) e \( t = 2 \)
- c) Ambas são crescentes, mas a exponencial cresce mais rápido
- d) Diferença para \( t = 3 \): 2000 bactérias