Função injetiva

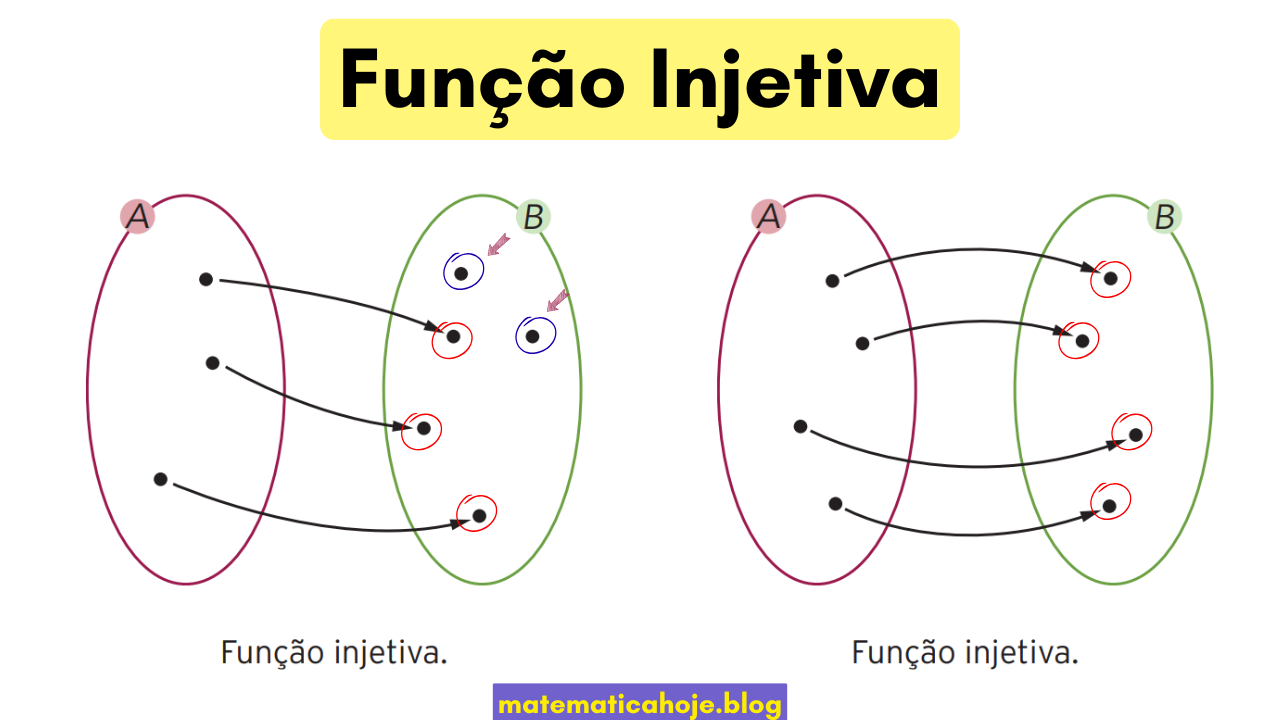
Uma função \(f:A\to B\) é injetiva (ou um–para–um) quando valores distintos no domínio levam a valores distintos no contradomínio. Intuitivamente, nenhum elemento de \(B\) recebe duas “setas”.

Definições equivalentes

Critério 1 (pelo gráfico)
\(f\) é injetiva se e somente se qualquer reta horizontal corta o gráfico de \(y=f(x)\) em, no máximo, um ponto.

Critério 2 (lógico)
\[ \forall x_1,x_2\in A,\ f(x_1)=f(x_2)\ \Rightarrow\ x_1=x_2. \] Equivalente a: \(x_1\neq x_2 \Rightarrow f(x_1)\neq f(x_2)\).

Critério 3 (pré-imagem)
\[ \left|f^{-1}(\{y\})\right|\le 1,\qquad \forall\,y\in B. \]

Atalhos úteis

Monotonicidade: em intervalos, se \(f\) é estritamente crescente ou decrescente, então é injetiva.
Derivada: se \(f'(x)\) não troca de sinal (ex.: \(f'(x)>0\) ou \(f'(x)<0\) em todo o intervalo), então \(f\) é injetiva nesse intervalo.
Conjuntos finitos: se \(|A|>|B|\), nenhuma \(f:A\to B\) é injetiva (princípio das gavetas).
Composição: se \(f\) e \(g\) são injetivas, então \(g\circ f\) é injetiva; se \(g\circ f\) é injetiva, então \(f\) é injetiva.
Inversa à esquerda: \(f\) é injetiva \(\iff\) existe \(h:\operatorname{Im}f\to A\) tal que \(h\circ f=\operatorname{id}_A\).

Exemplos rápidos

\(f(x)=ax+b\) com \(a\neq0\) é injetiva em \(\mathbb{R}\).
\(g(x)=x^2\) não é injetiva em \(\mathbb{R}\) (pois \(g(1)=g(-1)\)), mas é injetiva em \([0,\infty)\) ou \((-\infty,0]\).
\(e^x\) é injetiva em \(\mathbb{R}\) (estritamente crescente).
\(\sin x\) não é injetiva em \(\mathbb{R}\), mas é injetiva em \([-\pi/2,\ \pi/2]\).
\(|x|\) não é injetiva em \(\mathbb{R}\), mas torna-se injetiva em \(x\ge 0\) ou \(x\le 0\).

📘 Quer um “cola-resumo” com notação e testes? Veja o eBook Fórmulas Matemática.

Demonstração-modelo (igualar imagens)

Para provar que \(f\) é injetiva, iguale as imagens e conclua \(x_1=x_2\). Ex.: \(f(x)=\dfrac{ax+b}{cx+d}\) com \(ad-bc\neq0\) (e \(cx+d\neq0\)).

Suponha \(f(x_1)=f(x_2)\):

\[ \frac{ax_1+b}{cx_1+d}=\frac{ax_2+b}{cx_2+d} \ \Rightarrow\ (ax_1+b)(cx_2+d)=(ax_2+b)(cx_1+d) \] \[ (ad-bc)(x_1-x_2)=0 \ \Rightarrow\ x_1=x_2. \]

Logo, \(f\) é injetiva no seu domínio.

Quadro-resumo

Como checar injetividade rapidamente
Ferramenta	Aplicação	Exemplo
Reta horizontal	Corta no máx. 1 ponto	Gráfico de \(e^x\)
Monotonicidade	\(f\) estritamente crescente/decrescente	\(ax+b\) com \(a\neq0\)
Derivada	\(f'(x)\) sem trocar sinal	\(\dfrac{ax+b}{cx+d}\) com \(ad-bc\neq0\)
Cardinalidade	\(\|A\|>\|B\|\Rightarrow\) não há injeção	5 → 4 elementos (impossível)
Restrição do domínio	Tornar \(f\) injetiva	\(x^2\) em \([0,\infty)\)

➡️ Praticar funções injetivas no Banco de Questões

Exercícios (múltipla escolha) com solução

1) Classifique quanto à injetividade em \(\mathbb{R}\): \(f(x)=3x-5\), \(g(x)=x^2-4\), \(h(x)=e^x\), \(p(x)=|x-1|\).

Todos são injetivos.
Apenas \(f\) e \(h\) são injetivos.
Apenas \(g\) e \(p\) são injetivos.
Apenas \(h\) é injetiva.

Ver solução

\(f\) (linear, \(a\neq0\)) é injetiva; \(h=e^x\) é injetiva; \(g\) e \(p\) não são em \(\mathbb{R}\). Alternativa: (b).

2) Dê um intervalo onde \(\sin x\) é injetiva.

\([-\pi,\ \pi]\)
\([-\pi/2,\ \pi/2]\)
\([0,\ 2\pi]\)
\([\pi/4,\ 5\pi/4]\)

Ver solução

Em qualquer intervalo de comprimento \(\pi\) onde é estritamente monótona. A clássica é \([-\pi/2,\ \pi/2]\).

3) Para que valores de \(k\) a função \(f(x)=x^3+kx\) é injetiva em \(\mathbb{R}\)?

Somente \(k>0\)
\(k\ge 0\)
\(k\le 0\)
Todos \(k\in\mathbb{R}\)

Ver solução

\(f'(x)=3x^2+k\). Se \(k\ge0\), \(f’\ge0\) e \(f\) é monótona (injetiva). Se \(k<0\), \(f’\) muda de sinal \(\Rightarrow\) não é injetiva. Resposta: \(k\ge0\).

4) Se \(f\) e \(g\) são injetivas, então \(g\circ f\) é:

Sempre injetiva.
Nunca injetiva.
Injetiva somente se \(g\) também for sobrejetiva.
Indefinida.

Ver solução

Se \((g\circ f)(x_1)=(g\circ f)(x_2)\Rightarrow g(f(x_1))=g(f(x_2))\stackrel{g\ \text{inj.}}{\Rightarrow} f(x_1)=f(x_2)\stackrel{f\ \text{inj.}}{\Rightarrow} x_1=x_2\). Logo, injetiva. Alternativa: (a).

5) Existe função injetiva \(f:A\to B\) com \(|A|=5\) e \(|B|=4\)?

Sim, basta \(B\) ser finito.
Não, pelo princípio das gavetas.
Sim, se \(A\) for subconjunto de \(B\).
Depende da imagem.

Ver solução

Com 5 elementos no domínio e 4 no contradomínio, dois elementos precisariam ter a mesma imagem. Não existe injeção. Alternativa: (b).

6) A função \(F(x)=\dfrac{ax+b}{cx+d}\) (\(ad-bc\ne0\)) é injetiva em seu domínio?

Não, pois é racional.
Sim, pois \(F'(x)=\dfrac{ad-bc}{(cx+d)^2}\) tem sinal constante.
Somente se \(a=d=0\).
Somente se \(b=c=0\).

Ver solução

\(F'(x)=\dfrac{ad-bc}{(cx+d)^2}\neq0\) e não muda de sinal no domínio \(\Rightarrow\) estritamente monótona \(\Rightarrow\) injetiva. Alternativa: (b).