Função Quadrática: o papel do coeficiente a

Função Quadrática: o que o coeficiente <em>a</em> faz no gráfico?

Função Quadrática: o papel do coeficiente a

Na função \(f(x)=ax^2+bx+c\) (\(a\neq0\)), o coeficiente \(a\) controla a concavidade e a abertura da parábola. Ele não determina sozinho a posição do vértice (porque \(y_v\) depende também de \(b\) e \(c\)), mas define se o vértice é mínimo ou máximo e o “quão aberto” é o gráfico.

1) Efeitos imediatos de \(a\)

Concavidade

\(a>0\): abre para cima (vértice é mínimo).
\(a<0\): abre para baixo (vértice é máximo).

Abertura (largura)

\(|a|\) grande → parábola mais estreita.
\(|a|\) pequeno → parábola mais larga.

Para \(y=ax^2\): \(x^2=4py\) \(\Rightarrow\) \(p=\dfrac{1}{4a}\). Quanto maior \(|a|\), menor \(p\) e mais “fechada”.

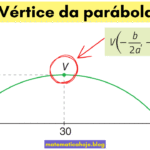
Vértice e eixo

\(x_v=-\dfrac{b}{2a}\) (o eixo \(x=x_v\) muda com \(a\) se \(b\neq0\)). Já \(y_v=-\dfrac{\Delta}{4a}\) troca de natureza com o sinal de \(a\).

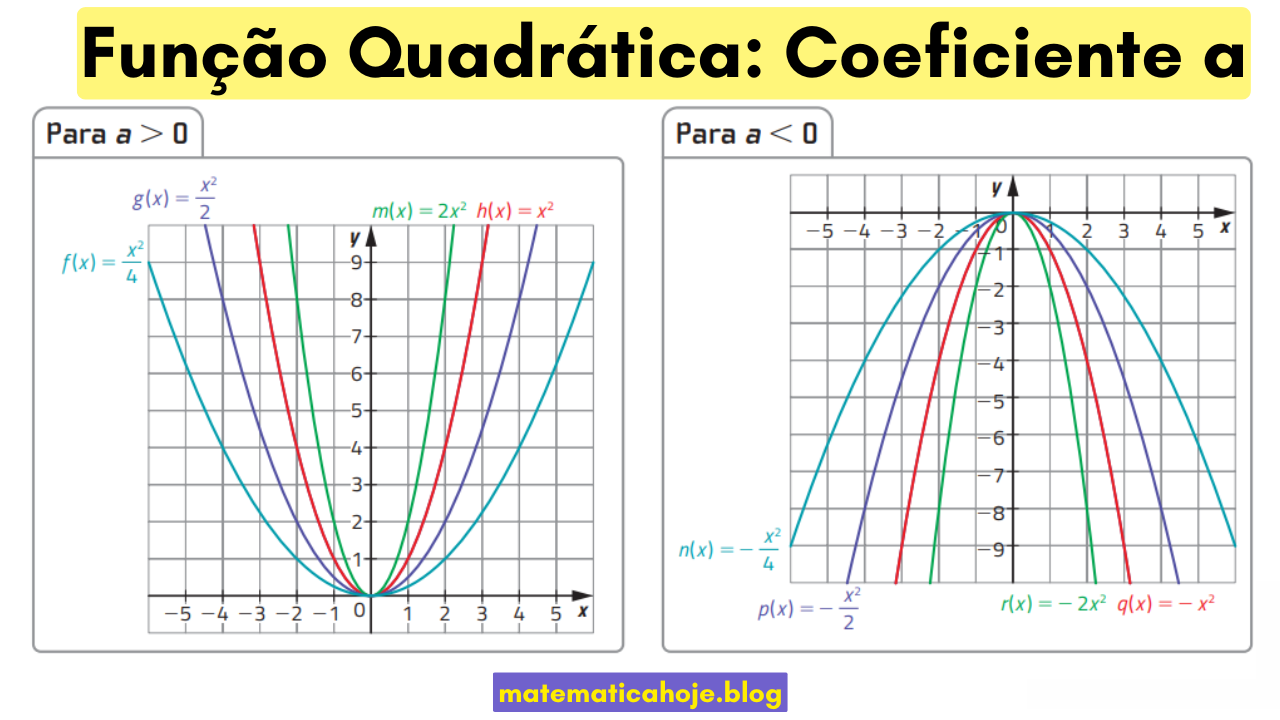
Comparação do efeito do coeficiente a no gráfico: parábolas abrindo para cima (a>0) e para baixo (a<0), mais estreitas e mais largas.

2) Visualizando com a família \(y=a(x-h)^2+k\)

Na forma canônica, \(a\) apenas estica/reflete a parábola em torno do eixo de simetria \(x=h\), sem mover o vértice \((h,k)\). Isso ajuda muito a esboçar rápido: comece da parábola básica \(y=(x-h)^2\), aplique o fator \(a\) e por fim translade \((h,k)\).

📘 E-book: Fórmulas de Matemática (referência rápida e completa)

Reforce os tópicos de função quadrática, equações, inequações e muito mais com um compilado organizado para consultas e revisões.

Acessar o E-book de Fórmulas

3) Exemplos resolvidos (contas uma embaixo da outra)

Exemplo A — Compare \(f_1(x)=\tfrac{1}{4}x^2\), \(f_2(x)=x^2\) e \(f_3(x)=4x^2\)

Quem é mais “aberta” e quem é mais “estreita”?

\[ \begin{aligned} a_1&=\tfrac{1}{4}\quad(|a_1|=0{,}25)\\ a_2&=1\quad(|a_2|=1)\\ a_3&=4\quad(|a_3|=4)\\[4pt] \text{Largura: }& |a_1|<|a_2|<|a_3|\\ &\Rightarrow f_1 \text{ é a mais larga, } f_3 \text{ a mais estreita.} \end{aligned} \]

Exemplo B — Natureza do vértice em \(g(x)=-2x^2+4x+6\)

\[ \begin{aligned} a&=-2\ (<0)\Rightarrow \text{concavidade para baixo}\\ x_v&=-\frac{b}{2a}=-\frac{4}{-4}=1\\ y_v&=g(1)=-2(1)^2+4(1)+6=-2+4+6=8 \end{aligned} \]

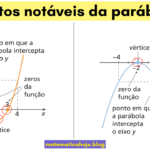
Como \(a<0\), o vértice \((1,8)\) é máximo. (Veja a análise completa deste exemplo no artigo pontos notáveis da parábola.)

Exemplo C — Mesmo \(b,c\), dois valores de \(a\)

Considere \(f_a(x)=ax^2-4x+1\). Compare o eixo e o vértice para \(a=1\) e \(a=4\).

\[ \begin{aligned} \text{Para } a=1:&\\ x_v&=-\frac{-4}{2\cdot 1}=2\\ y_v&=f_1(2)=1\cdot 4-8+1= -3\\[6pt] \text{Para } a=4:&\\ x_v&=-\frac{-4}{2\cdot 4}= \frac{1}{2}\\ y_v&=f_4\!\left(\tfrac{1}{2}\right)=4\left(\tfrac{1}{4}\right)-4\left(\tfrac{1}{2}\right)+1\\ &=1-2+1\\ &=0 \end{aligned} \]

Alterar \(a\) mudou o eixo de simetria (pois \(x_v=-b/2a\)) e a altura do vértice.

4) Perguntas rápidas

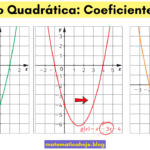
\(a\) altera o intercepto em \(y\)? Não diretamente; o intercepto é \((0,c)\).
\(a\) muda as raízes? Sim, pois a expressão de Bhaskara usa \(\Delta=b^2-4ac\) (há \(a\) no produto \(ac\)) e o denominador \(2a\).
\(a\) muda só a “abertura” na forma \(y=a(x-h)^2+k\)? Sim; nessa forma, o vértice \((h,k)\) e o eixo \(x=h\) não mudam quando variamos \(a\).

5) Exercícios propostos (com gabarito)

1) Classifique a concavidade e o tipo de vértice de \(f(x)=3x^2-6x+2\). Calcule \(x_v\) e \(y_v\).

Gabarito

\[ \begin{aligned} a&=3>0\Rightarrow \text{abre para cima (vértice mínimo)}\\ x_v&=-\frac{-6}{2\cdot 3}=1\\ y_v&=f(1)=3(1)-6(1)+2=3-6+2=-1 \end{aligned} \]

2) Para \(g(x)=-\tfrac12 x^2+2x-5\): concavidade, largura em relação a \(y=-x^2\) e vértice.

Gabarito

\[ \begin{aligned} a&=-\tfrac12<0\Rightarrow \text{abre para baixo (vértice máximo)}\\ |a|&=0{,}5<1\Rightarrow \text{mais larga que } y=-x^2\\ x_v&=-\frac{2}{2(-\tfrac12)}=-\frac{2}{-1}=2\\ y_v&=g(2)=-\tfrac12(4)+2(2)-5=-2+4-5=-3 \end{aligned} \]

3) Determine o valor de \(a\) para que \(h(x)=a(x-1)^2+3\) seja mais estreita que \(y=(x-1)^2+3\) e abra para cima.

Gabarito

Abra para cima \(\Rightarrow a>0\). Mais estreita que \(1\) \(\Rightarrow |a|>1\). Assim, \(a>1\).

6) Continue estudando

Função Quadrática (guia completo) Gráfico da quadrática A parábola (foco e diretriz) Pontos notáveis da parábola Inequações produto Inequações quociente

Relacionadas

Soma e Produto das Raízes da Equação do 2º Grau

Estudo do sinal da Função Quadrática

Variação de sinal da função quadrática

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.