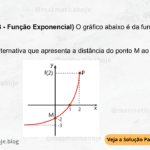
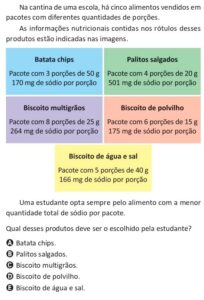
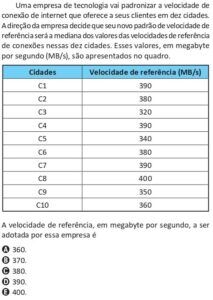
24. Copie o quadro a seguir, referente às funções definidas por \( f(x) = 3^x \), \( g(x) = 3^x + 2 \) e \( h(x) = 3^{x-2} \), e complete-o:
| Lei da função | x | -2 | -1 | 0 | 1 | 2 | 3 |
| \( f(x) = 3^x \) | |||||||
| \( g(x) = 3^x + 2 \) | |||||||
| \( h(x) = 3^{x – 2} \) |
Agora, faça o que se pede:
- Utilizando o GeoGebra, construa, em um mesmo sistema cartesiano, o gráfico de \( f \), de \( g \) e de \( h \).
- Ao analisar os gráficos construídos, podemos dizer que \( f \), \( g \) e \( h \) são funções crescentes ou decrescentes?
- Determine o domínio e o conjunto imagem dessas funções.
- Descreva como seria o gráfico da função dada por \( m(x) = 3^x – 2 \), em relação ao gráfico de \( f \), sem construí-lo.
- Descreva como seria o gráfico da função dada por \( q(x) = 3^{x + 2} \), em relação ao gráfico de \( f \), sem construí-lo.
- Construa, em um mesmo sistema cartesiano, os gráficos das funções \( f \), \( m \) e \( q \), e comprove as respostas dadas nos itens d e e.
🔍 Ver solução passo a passo
| Lei da função | x | -2 | -1 | 0 | 1 | 2 | 3 |
| \( f(x) = 3^x \) | \( \dfrac{1}{9} \) | \( \dfrac{1}{3} \) | 1 | 3 | 9 | 27 | |
| \( g(x) = 3^x + 2 \) | \( \dfrac{1}{9} + 2 \) | \( \dfrac{1}{3} + 2 \) | 1 + 2 | 3 + 2 | 9 + 2 | 27 + 2 | |
| \( h(x) = 3^{x – 2} \) | \( \dfrac{1}{81} \) | \( \dfrac{1}{27} \) | \( \dfrac{1}{9} \) | \( \dfrac{1}{3} \) | 1 | 3 |
a) A construção pode ser feita com o software GeoGebra, inserindo os comandos:
f(x) = 3^xg(x) = 3^x + 2h(x) = 3^(x - 2)
b) Todas as funções são exponenciais com base \( > 1 \).
✅ Resposta: As funções \( f \), \( g \) e \( h \) são crescentes.
c)
- Domínio: \( D(f) = D(g) = D(h) = \mathbb{R} \)
- Imagem:
\( \text{Im}(f) = \mathbb{R}_+^* \)
\( \text{Im}(g) = \{ y \in \mathbb{R} \mid y > 2 \} \)
\( \text{Im}(h) = \mathbb{R}_+^* \)
d) A função \( m(x) = 3^x – 2 \) é uma translação vertical para baixo do gráfico de \( f(x) = 3^x \).
Ou seja, cada ponto do gráfico de \( f \) é deslocado 2 unidades para baixo.
e) A função \( q(x) = 3^{x+2} \) representa uma translação horizontal para a esquerda do gráfico de \( f(x) = 3^x \), deslocando-o 2 unidades para a esquerda.
f) Ao construir os gráficos de \( f \), \( m \) e \( q \), podemos visualizar:
- \( m(x) \): gráfico mais abaixo, mesma forma que \( f \)
- \( q(x) \): gráfico deslocado para a esquerda
Esses deslocamentos confirmam as transformações descritas nos itens anteriores.
✅ Conclusão geral:
- \( f \), \( g \), \( h \), \( m \) e \( q \) são todas funções exponenciais crescentes
- Transformações em \( f \) afetam posição, mas não o crescimento
- Domínios continuam \( \mathbb{R} \), e as imagens variam conforme a translação vertical