Interpolação Aritmética
Interpolar (inserir) k meios aritméticos entre a e b significa construir uma P.A. cujos extremos são a₁ = a e aₙ = b, com n = k + 2. Conteúdo muito cobrado em provas e no ENEM.
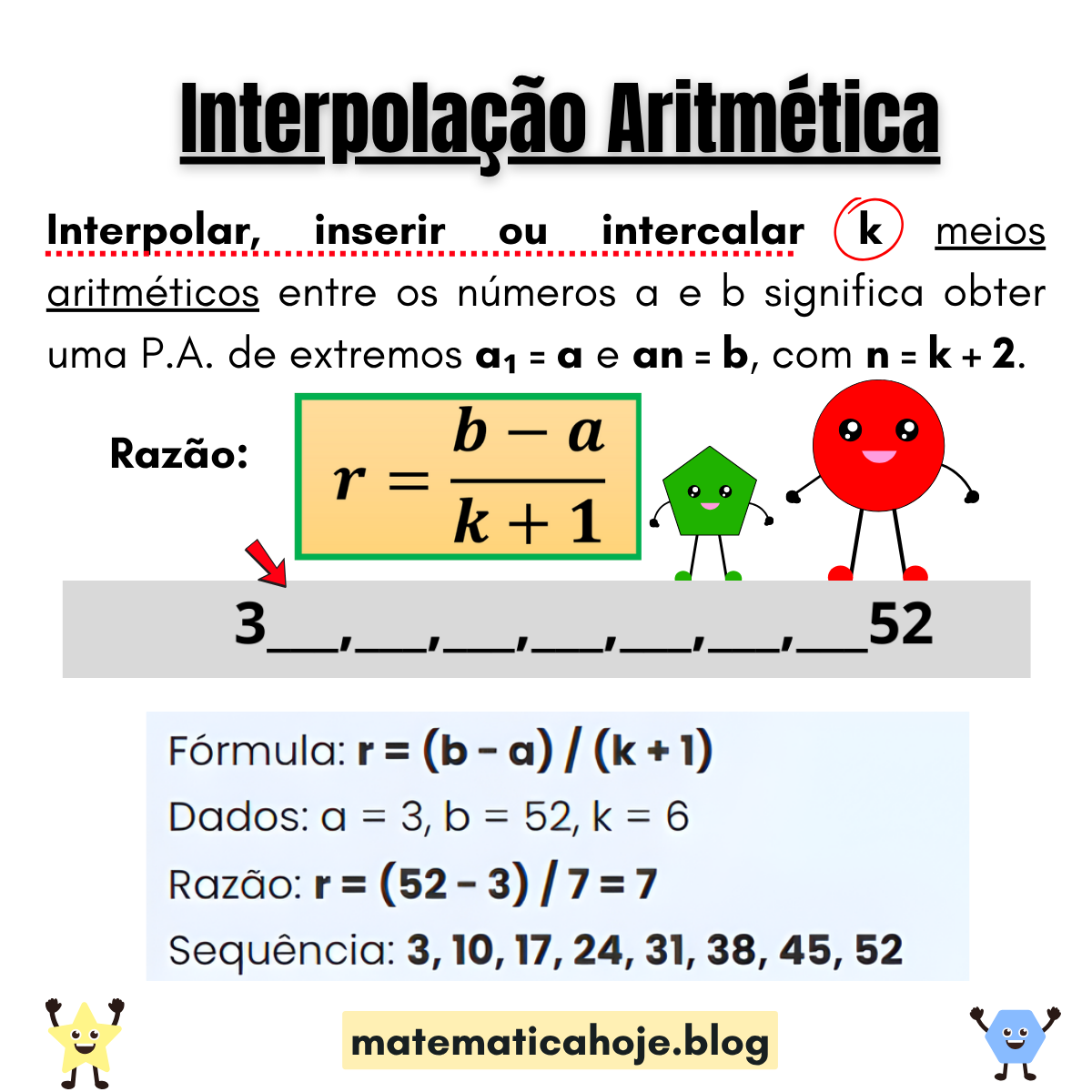
📘 Fórmula da razão
Com a razão r encontrada, gera-se a sequência somando r sucessivamente a partir de a até chegar a b.
Revisões úteis: Definição de P.A. • Classificação • Termo Geral • Propriedade Fundamental
📗 Baixe grátis o eBook Fórmulas Matemática
Todas as fórmulas de P.A., P.G., Funções, Geometria e Estatística com quadros-resumo e exemplos. Ótimo para revisão rápida.
📥 Baixar agora💡 Exemplo resolvido — inserir 6 meios entre 3 e 52
a = 3, b = 52, k = 6
r = (b − a)/(k + 1) = (52 − 3)/7 = 7
Termos:
a₁ = 3
a₂ = 3 + 7 = 10
a₃ = 10 + 7 = 17
a₄ = 17 + 7 = 24
a₅ = 24 + 7 = 31
a₆ = 31 + 7 = 38
a₇ = 38 + 7 = 45
a₈ = 45 + 7 = 52
Sequência final: 3, 10, 17, 24, 31, 38, 45, 52
🧠 Mapas Mentais de Matemática: visualize “Interpolação”, “Termo Geral” e “Classificação” de P.A. em cartões-resumo.
🔗 Continue estudando
🧩 Lista de Exercícios — Interpolação Aritmética
Metade em múltipla escolha e metade discursiva. Clique em ver solução para abrir o passo a passo.
1) (Múltipla escolha) Insira 3 meios aritméticos entre 2 e 14. A razão r é:
👀 Ver solução
a=2, b=14, k=3
r=(14−2)/(3+1)=12/4=3
Sequência: 2, 5, 8, 11, 14
2) (Múltipla escolha) Entre −10 e 8 inserem-se 5 meios. O 4º termo da P.A. é:
👀 Ver solução
a=−10, b=8, k=5
r=(8−(−10))/(5+1)=18/6=3
Termos: −10, −7, −4, −1, 2, 5, 8 ⇒ 4º termo (a₄)=−1? (Atenção)
Contando: a₁=−10, a₂=−7, a₃=−4, a₄=−1 ⇒ Alternativa correta deve ser −1.
Se a lista da questão pedir “3º termo interno” (1º meio), seria −7.
(Use o enunciado como acima: 4º termo da P.A. = −1.)
3) (Discursiva) Inserir 4 meios entre 6 e 36 e escrever a sequência completa.
👀 Ver solução
a=6, b=36, k=4
r=(36−6)/(4+1)=30/5=6
6, 12, 18, 24, 30, 36
4) (Discursiva) Entre 5 e 41, inserem-se k meios aritméticos e obtém-se r = 3. Determine k e escreva os dois primeiros meios.
👀 Ver solução
r=(b−a)/(k+1) ⇒ 3=(41−5)/(k+1)=36/(k+1)
k+1=12 ⇒ k=11
Meios (a partir de 5 somando 3): 8, 11, 14, ...













