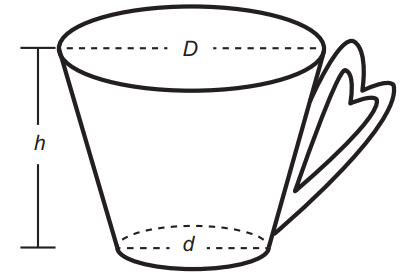
Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.
Sabe-se que 1 cm³ = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm.
Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).
Utilize 3 como aproximação para π.
Qual é a capacidade volumétrica, em mililitro, dessa caneca?
- 216.
- 408.
- 732.
- 196.
- 228.
Mostrar / esconder solução passo a passo
1) Modelagem
A caneca é um tronco de cone com altura \(h=12\) cm, raio do topo \(R=\frac{D}{2}=5\) cm e raio da base \(r=\frac{d}{2}=4\) cm.
2) Fórmula do volume
\[
V=\frac{h}{3}\,\pi\,(R^{2}+Rr+r^{2}).
\]
Com \(\pi\approx 3\):
\[
V=\frac{12}{3}\cdot 3 \cdot (5^{2}+5\cdot 4+4^{2})
=4\cdot 3 \cdot (25+20+16)
=12\cdot 61
=\boxed{732}\ \text{cm}^{3}.
\]
Como \(1\ \text{cm}^3 = 1\ \text{mL}\), a capacidade é 732 mL ⇒ letra C.
Página desta questão
ENEM 2021 — Matemática — Questão 12
.
Banco de Questões do ENEM (Matemática)
acessar agora.
Mapas Mentais de Matemática
ver mapas.
10 eBooks de Matemática
baixar eBooks.