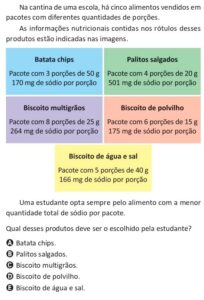
a) \( f(x) = \sqrt{2^x – 2^{1 – x}} \)
🔍 Ver solução da letra a)
🔎 Etapa 1 – Condição de existência da raiz quadrada:
Para que \( f(x) \) seja real, o radicando deve ser maior ou igual a zero:
$$ 2^x – 2^{1 – x} \geq 0 $$
🔎 Etapa 2 – Igualando bases:
\( 2^{1 – x} = \dfrac{2}{2^x} \), então:
$$ 2^x – \dfrac{2}{2^x} \geq 0 $$
🔎 Etapa 3 – Multiplicando ambos os lados por \( 2^x \gt 0 \):
$$ (2^x)^2 – 2 \geq 0 \Rightarrow 2^{2x} \geq 2 $$
Como \( 2 = 2^1 \), temos: $$ 2x \geq 1 \Rightarrow x \geq \dfrac{1}{2} $$
✅ Domínio de f(x):
- \( D(f) = \{ x \in \mathbb{R} \mid x \geq \dfrac{1}{2} \} \)
b) \( g(x) = \sqrt{(0{,}1)^{x^2 – 5x} – (0{,}1)^{-6}} \)
🔍 Ver solução da letra b)
🔎 Etapa 1 – Igualando expoentes:
\( (0{,}1)^{-6} = \dfrac{1}{(0{,}1)^6} \), e como \( 0{,}1 = 10^{-1} \), temos: $$ (0{,}1)^a \geq (0{,}1)^b \Leftrightarrow a \leq b $$ pois \( 0{,}1 \in (0,1) \) → base entre 0 e 1.
Logo, para que o radicando seja ≥ 0, devemos ter:
$$ (0{,}1)^{x^2 – 5x} \geq (0{,}1)^{-6} \Rightarrow x^2 – 5x \leq -6 $$
🔎 Etapa 2 – Resolvendo a inequação:
$$ x^2 – 5x + 6 \leq 0 $$
Raízes: \( x = 2 \) e \( x = 3 \)
Intervalo solução: $$ x \in [2, 3] $$
✅ Domínio de g(x):
- \( D(g) = \{ x \in \mathbb{R} \mid 2 \leq x \leq 3 \} \)