Sinal da função: como decidir onde é positivo, negativo ou zero
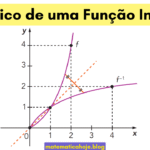
Sinal da função descreve, para cada \(x\), se \(f(x)\) é positivo \((\gt0)\), negativo \((\lt0)\) ou zero. No gráfico, é simples: o traço acima do eixo \(x\) indica \(f(x)\gt 0\); abaixo, \(f(x)\lt 0\); tocando o eixo, \(f(x)=0\). Relembre também: zero (raiz/intercepto-x), estudo do sinal para função afim, crescente x decrescente e gráfico do 1º grau.
Definição rápida
Regras úteis
- Função afim \(f(x)=ax+b\) \((a\ne 0)\): zero em \(x_0=-\dfrac{b}{a}\). Se \(a\gt0\), \(f(x)\gt0\) para \(x\gt x_0\) e \(f(x)\lt0\) para \(x\lt x_0\). Se \(a\lt0\), inverta. Casos especiais: linear (\(b=0\)) e constante (\(a=0\)).
- Polinômios fatorados: se \(f(x)=k\prod (x-r_i)^{m_i}\) e \(k\ne0\),
- ao passar por uma raiz de multiplicidade ímpar o sinal muda;
- em multiplicidade par a curva “toca” o eixo e o sinal não muda;
- o sinal “longe” varia como o de \(k\cdot x^{\text{grau}}\).
- Racionais \(\dfrac{N(x)}{D(x)}\): o sinal é o do numerador vezes o sinal do denominador; pontos onde \(D(x)=0\) não pertencem ao domínio (assíntotas verticais) e dividem os intervalos de teste.
Exemplos resolvidos
Exemplo 1 — Quadrática clássica. Determine onde \(f(x)=x^2-9\) é positiva, negativa e nula.
Ver solução
Fatores: \(f(x)=(x-3)(x+3)\). Zeros em \(-3\) e \(3\) (ambos ímpares ⇒ troca de sinal em cada). Para \(x\gt 3\), \(f\gt0\) (abre para cima). Logo: \(\ f(x)\gt0\) em \((-\infty,-3)\cup(3,\infty)\); \(\ f(x)=0\) em \(\{-3,3\}\); \(\ f(x)\lt0\) em \((-3,3)\).
Exemplo 2 — Multiplicidade par. Analise \(g(x)=(x-2)^2(x+1)\).
Ver solução
Raízes: \(x=-1\) (ímpar) e \(x=2\) (par). Para \(x\to+\infty\), \(g\gt0\). Assim, \(g\lt0\) em \((-\infty,-1)\), \(g=0\) em \(-1\), \(g\gt0\) em \((-1,2)\cup(2,\infty)\) e \(g=0\) em \(2\). O sinal não muda ao atravessar \(x=2\).
Exemplo 3 — Função afim. Para \(h(x)=-2x+5\), encontre onde \(h\) é positiva e negativa.
Ver solução
Zero \(x_0=-b/a=-5/(-2)=2{,}5\). Como \(a\lt0\) ⇒ \(h\gt0\) para \(x\lt2{,}5\) e \(h\lt0\) para \(x\gt2{,}5\). Veja o quadro do sinal da afim.
Exemplo 4 — Função racional. Analise o sinal de \(p(x)=\dfrac{x-1}{x+2}\).
Ver solução
Domínio: \(x\ne-2\). Zeros/assíntotas: zero em \(x=1\); assíntota em \(x=-2\). Testando intervalos: \((-\infty,-2)\Rightarrow (+)\); \((-2,1)\Rightarrow (-)\); \((1,\infty)\Rightarrow (+)\). Logo \(p\gt0\) em \((-\infty,-2)\cup(1,\infty)\), \(p=0\) em \(\{1\}\), \(p\lt0\) em \((-2,1)\).
Quadro do sinal (exemplo 1)
| Intervalo | \((-\infty,-3)\) | \(\{-3\}\) | \((-3,3)\) | \(\{3\}\) | \((3,\infty)\) |
|---|---|---|---|---|---|
| Sinal de \(x^2-9\) | + | 0 | − | 0 | + |
Erros comuns
- Confundir altura (valor de \(y\)) com crescimento. Sinal indica se está acima/abaixo do eixo, não se está subindo/descendo (veja crescente/decrescente).
- Esquecer as restrições do domínio (como \(x=-2\) em racionais).
- Ignorar a multiplicidade: raízes pares não trocam o sinal.
Exercícios propostos (com gabarito)
1) Determine o sinal de \(f(x)=\dfrac{(x-3)(x+2)}{x-1}\) e indique domínio e zeros.
Gabarito
Domínio: \(x\ne1\). Zeros em \(x=3\) e \(x=-2\). Sinais por intervalos: \((-\infty,-2): (+)/(−)\Rightarrow (−)\); \((-2,1): (−)/(−)\Rightarrow (+)\); \((1,3): (+)/(+)\Rightarrow (+)\); \((3,\infty): (+)/(+)\Rightarrow (+)\). Trocas nos zeros de multiplicidade ímpar e na assíntota \(x=1\).
2) Para \(g(x)=(x+1)^2(x-4)\), construa o quadro do sinal.
Gabarito
Raízes: \(-1\) (par, não troca), \(4\) (ímpar, troca). Como o grau é 3 e o coeficiente líder é \(+\), o sinal em \(+\infty\) é \(+\). Logo: \((-\infty,-1): (-)\); \(\{-1\}: 0\); \((-1,4): (-)\) (não troca); \(\{4\}: 0\); \((4,\infty): (+)\).
3) Para a afim \(h(x)=1{,}2x-0{,}6\), determine onde é positiva, nula e negativa.
Gabarito
Zero \(x_0=-b/a=0{,}5\). Como \(a\gt0\): \(h\lt0\) em \((-\infty,0{,}5)\), \(h=0\) em \(0{,}5\), \(h\gt0\) em \((0{,}5,\infty)\).
4) Para \(q(x)=\dfrac{x-2}{(x-1)^2}\), discuta o sinal e os pontos proibidos.
Gabarito
Domínio: \(x\ne1\). O fator \((x-1)^2\) é sempre \(>0\) (exceto no ponto proibido). Logo o sinal é o de \(x-2\): negativo em \((-\infty,2)\), zero em \(2\), positivo em \((2,\infty)\).
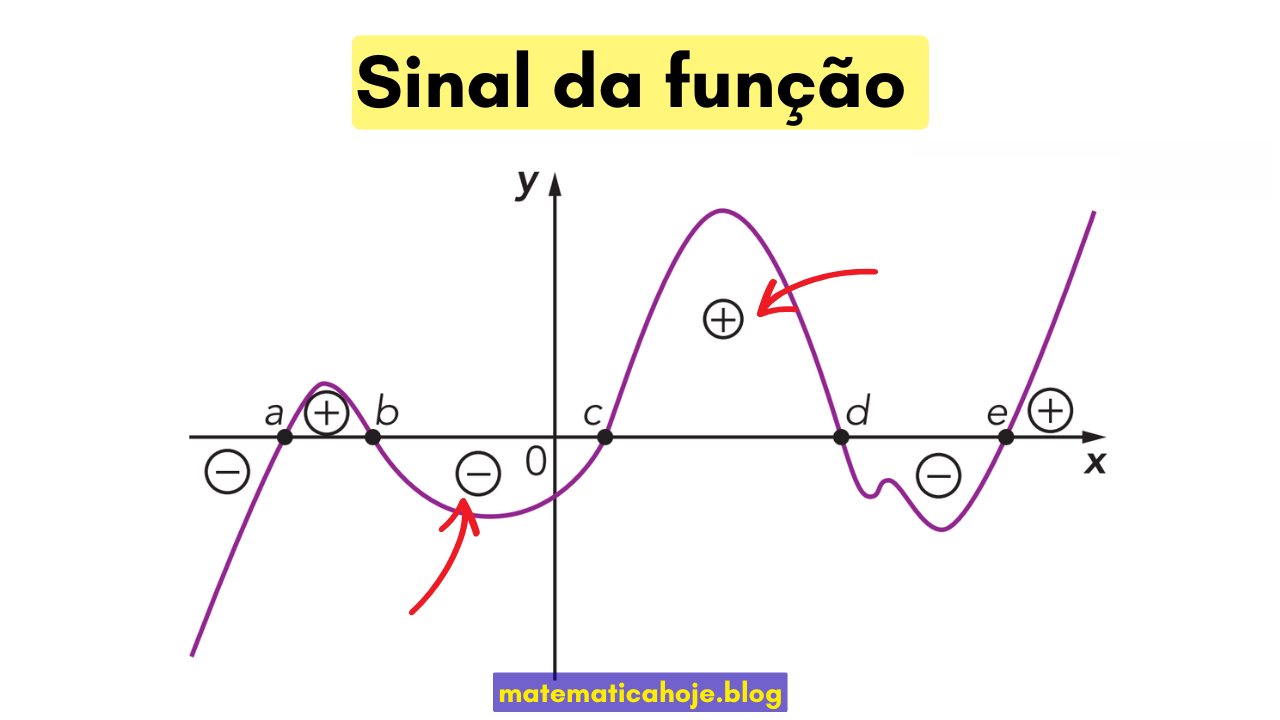
5) A figura do topo marca \(a<b<c<d<e\) como zeros. Copie os intervalos e escreva qual é o sinal de \(f\) em cada um.
Gabarito
Da esquerda para a direita, usando a imagem: \((-\infty,a)\): −; \((a,b)\): +; \((b,c)\): −; \((c,d)\): +; \((d,e)\): −; \((e,\infty)\): +.