Método da Adição (Eliminação) — Sistemas Lineares
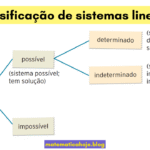
O método da adição (também chamado de eliminação) consiste em somar equações convenientemente para eliminar uma incógnita. Em sistemas \(2\times2\) basta tornar os coeficientes de uma variável opostos e somar; em \(3\times3\) fazemos duas eliminações e reduzimos a um \(2\times2\). Para revisar conteúdos relacionados: método da substituição, eliminação de Gauss, solução de um sistema linear e classificação (SPD, SI, SPI).

📘 eBook Fórmulas Matemática — seu guia rápido de Sistemas
Passo a passo do método da adição, substituição, Gauss/Gauss–Jordan, critérios SPD–SI–SPI e forma vetorial/paramétrica.
Quero o eBook Praticar no Banco de QuestõesPasso a passo do método da adição
- Escolha a variável a eliminar (ex.: \(y\)).
- Torne os coeficientes dessa variável opostos (multiplicando alguma equação, se necessário).
- Some as equações: a variável escolhida desaparece.
- Resolva a equação resultante; volte para achar a outra incógnita.
- Verifique nas equações originais.
Dica: Se os coeficientes já são opostos, some direto. Se são iguais, subtraia.
Exemplo 1 — SPD (soma direta elimina \(y\))
\(\begin{cases}3x+5y=2\\ 2x-5y=18\end{cases}\)
Resolver
Somando: \( (3x+5y)+(2x-5y)=2+18 \Rightarrow 5x=20 \Rightarrow x=4\). Em \(3x+5y=2\Rightarrow 12+5y=2\Rightarrow 5y=-10\Rightarrow y=-2\). Solução: \((4,-2)\).
Exemplo 2 — Tornando opostos antes de somar
\(\begin{cases}4x+3y=17\\ 5x+2y=14\end{cases}\)
Resolver
Quero eliminar \(y\). Faça \(L_1\times2\) e \(L_2\times(-3)\): \( \{\,8x+6y=34,\ -15x-6y=-42\,\}\). Somando: \(-7x=-8\Rightarrow x=\tfrac{8}{7}\). Em \(5x+2y=14\Rightarrow 5\cdot\tfrac{8}{7}+2y=14\Rightarrow \tfrac{40}{7}+2y=14\Rightarrow 2y=\tfrac{58}{7}\Rightarrow y=\tfrac{29}{7}\). Solução: \(\left(\tfrac{8}{7},\tfrac{29}{7}\right)\).
Exemplo 3 — SPI (infinitas soluções)
\(\begin{cases}2x+4y=8\\ -x-2y=-4\end{cases}\)
Diagnóstico
Multiplique a 2ª por \(2\): \(-2x-4y=-8\). Somando com a 1ª: \(0=0\) ⇒ as equações são proporcionais ⇒ SPI. Da 1ª: \(2x=8-4y\Rightarrow x=4-2y\). Parametrize \(y=t\): \((x,y)=(4-2t,t)\).
Exemplo 4 — SI (sem solução)
\(\begin{cases}2x+4y=8\\ -x-2y=-3\end{cases}\)
Diagnóstico
Multiplique a 2ª por \(2\): \(-2x-4y=-6\). Somando com a 1ª: \(0=2\) ⇒ contradição ⇒ SI.
Exemplo 5 — \(3\times3\) por adição (duas eliminações)
\(\begin{cases}x+y+z=6\\ 2x-y+z=7\\ -x+2y-z=0\end{cases}\)
Resolver
Eliminar \(z\). (1)+(3): \(x+y+z + (-x+2y-z)=3y=6 \Rightarrow y=2\). (2)+(3): \(2x-y+z + (-x+2y-z)=x+y=7 \Rightarrow x=7-y=5\). Em (1): \(5+2+z=6\Rightarrow z=-1\). Solução: \((5,2,-1)\).
Exercícios (método da adição)
1) \(\{\,3x+2y=11,\; 5x-2y=9\,\}\)
Gabarito
Somando: \(8x=20\Rightarrow x=2.5\). Em 1ª: \(7+2y=11\Rightarrow y=2\). \(\,(x,y)=(2.5,2)\)
2) \(\{\,4x-3y=5,\; 6x+5y=31\,\}\)
Gabarito
Torne \(y\) oposto: \(L_1\times5\Rightarrow 20x-15y=25\); \(L_2\times3\Rightarrow 18x+15y=93\). Somando: \(38x=118\Rightarrow x=\tfrac{59}{19}=3.1053…\) Ops: melhor usar outra eliminação. Eliminando \(x\): \(L_1\times3\Rightarrow 12x-9y=15\); \(L_2\times(-2)\Rightarrow -12x-10y=-62\). Somando: \(-19y=-47\Rightarrow y=\tfrac{47}{19}=\mathbf{2.473684…}\). Em \(4x-3y=5\Rightarrow 4x-3\cdot\tfrac{47}{19}=5\Rightarrow 4x=\tfrac{142}{19}\Rightarrow x=\tfrac{71}{38}\). Solução exata: \(x=\tfrac{71}{38},\ y=\tfrac{47}{19}\).
3) \(\{\,x+4y=1,\; 3x-4y=11\,\}\)
Gabarito
Somando: \(4x=12\Rightarrow x=3\). Em 1ª: \(3+4y=1\Rightarrow y=-\tfrac{1}{2}\).
4) (SPI) \(\{\,x-2y=3,\; 2x-4y=6\,\}\)
Gabarito
2ª é o dobro da 1ª. Somando com \(-(2)\): \(0=0\). Infinitas: \(x=3+2t,\ y=t\).
5) (SI) \(\{\,x-2y=3,\; 2x-4y=7\,\}\)
Gabarito
Dobrando a 1ª teríamos \(2x-4y=6\neq7\). Contradição ⇒ sem solução.
6) \(3\times3:\ \{\,x+2y+z=9,\; 2x-y+z=8,\; -x+y-z= -1\,\}\)
Gabarito
Elimine \(z\): (1)+(3) ⇒ \(x+3y=8\). (2)+(3) ⇒ \(x=7\). Volte: \(7+3y=8⇒y=\tfrac{1}{3}\). Em (1): \(7+2\cdot\tfrac{1}{3}+z=9⇒ \tfrac{21}{3}+\tfrac{2}{3}+z=\tfrac{27}{3}⇒ z=\tfrac{4}{3}\). Solução: \(\left(7,\tfrac{1}{3},\tfrac{4}{3}\right)\).
Leia também
Conclusão
O método da adição é rápido quando conseguimos coeficientes opostos para alguma variável. Combine-o com substituição e com Gauss para resolver qualquer sistema que apareça em provas.
Para ter um resumo de bolso com fórmulas e passos: eBook Fórmulas Matemática, e pratique no Banco de Questões.