O Teorema de Pitágoras é um dos conceitos mais conhecidos e amplamente aplicados na matemática, especialmente na geometria. Este teorema não só é fundamental para a resolução de problemas relacionados a triângulos retângulos, mas também tem inúmeras aplicações práticas em áreas como engenharia, arquitetura e física. Neste artigo, vamos explorar o Teorema de Pitágoras em detalhes, discutindo seu enunciado, provas e aplicações no mundo real.
O Que é o Teorema de Pitágoras?
O Teorema de Pitágoras é uma relação fundamental em geometria que envolve os comprimentos dos lados de um triângulo retângulo. Ele é nomeado em homenagem ao matemático grego Pitágoras, que é creditado com sua descoberta, embora o conhecimento do teorema provavelmente existisse em várias culturas antes dele.
Enunciado do Teorema de Pitágoras:
“Em um triângulo retângulo, o quadrado da medida da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados das medidas dos catetos.”
Matematicamente, isso é expresso como:

onde:
- a é a medida da hipotenusa,
- b e c são as medidas dos catetos.
Provas do Teorema de Pitágoras
O Teorema de Pitágoras pode ser provado de várias maneiras, incluindo provas geométricas, algébricas e até mesmo por meio de rearranjos de figuras. Aqui estão duas provas populares:
1. Prova Geométrica Clássica
Esta prova é baseada na área. Considere um triângulo retângulo com catetos b e c, e hipotenusa a. Se construirmos quadrados sobre cada um dos lados do triângulo, a área do quadrado maior (construído sobre a hipotenusa) será igual à soma das áreas dos dois quadrados menores (construídos sobre os catetos).
Área do quadrado sobre a=a2
Área do quadrado sobre b=b2
Área do quadrado sobre c=c2

2. Prova por Rearranjo
Outra prova envolve o rearranjo de triângulos. Desenhando quatro triângulos retângulos congruentes em torno de um quadrado central, podemos mostrar que a área do quadrado sobre a hipotenusa é igual à soma das áreas dos quadrados sobre os catetos, simplesmente rearranjando as peças.

Lista de Exercícios Resolvidos: Teorema de Pitágoras
Exercício 1:
Um triângulo retângulo tem os catetos medindo 3 cm e 4 cm. Qual é a medida da hipotenusa?
Resolução: Usando o Teorema de Pitágoras:

Resposta: A hipotenusa mede 5 cm.
Exercício 2:
Em um triângulo retângulo, a hipotenusa mede 13 cm e um dos catetos mede 5 cm. Calcule o outro cateto.
Resolução: Usando o Teorema de Pitágoras:
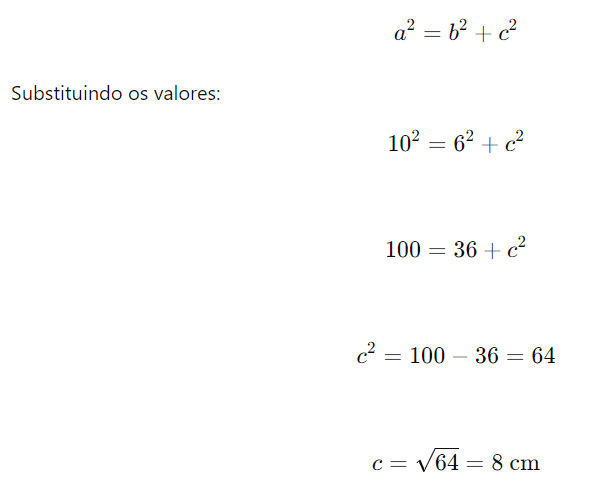
Resposta: O outro cateto mede 8 cm.
Exercício 4:
Em um triângulo retângulo, os catetos medem 8 cm e 15 cm. Qual é o comprimento da hipotenusa?
Resolução: Usando o Teorema de Pitágoras:

Resposta: A hipotenusa mede 17 cm.
xercício 5:
Um terreno retangular tem 30 metros de comprimento e 40 metros de largura. Qual é a diagonal do terreno?
Resolução: A diagonal do terreno forma a hipotenusa de um triângulo retângulo, onde os lados são o comprimento e a largura. Aplicando o Teorema de Pitágoras:
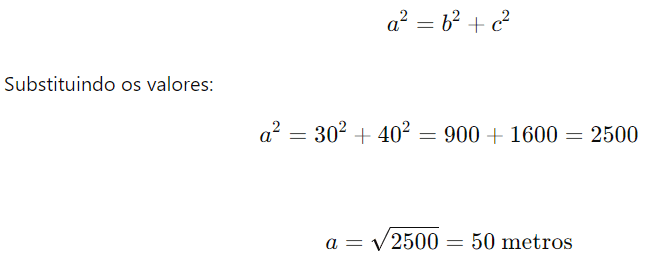
Resposta: A diagonal do terreno mede 50 metros.
Aplicações do Teorema de Pitágoras
O Teorema de Pitágoras tem diversas aplicações práticas, tanto em problemas teóricos quanto no mundo real. Aqui estão algumas delas:
1. Cálculo de Distâncias
Uma das aplicações mais comuns do Teorema de Pitágoras é no cálculo de distâncias. Por exemplo, se você conhece a altura de uma torre e a distância horizontal a partir de um ponto ao pé da torre, pode usar o teorema para calcular a distância direta (a hipotenusa) entre o ponto e o topo da torre.
2. Engenharia e Arquitetura
Engenheiros e arquitetos frequentemente utilizam o Teorema de Pitágoras para garantir que as estruturas sejam construídas corretamente. Ao criar esquadros perfeitos ou ao calcular comprimentos de vigas diagonais, o teorema é uma ferramenta indispensável.
3. Navegação e GPS
Em sistemas de navegação, como o GPS, o Teorema de Pitágoras é usado para calcular a posição exata de um objeto. Ao conhecer as distâncias de um objeto a partir de múltiplos pontos de referência, é possível determinar a localização precisa desse objeto no espaço.
4. Física e Astronomia
Na física, o teorema é usado em diversos contextos, como no cálculo da resultante de forças perpendiculares ou na determinação da distância entre dois pontos em coordenadas cartesianas. Na astronomia, ele ajuda a calcular distâncias entre corpos celestes.
Conclusão
O Teorema de Pitágoras é um pilar central da geometria e tem aplicações que vão muito além da sala de aula. Sua simplicidade e versatilidade o tornam uma ferramenta poderosa para resolver problemas práticos em diversas disciplinas. Seja para medir distâncias, desenhar projetos arquitetônicos ou entender conceitos de física, o Teorema de Pitágoras continua a ser uma das fórmulas mais úteis e fascinantes da matemática.
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes