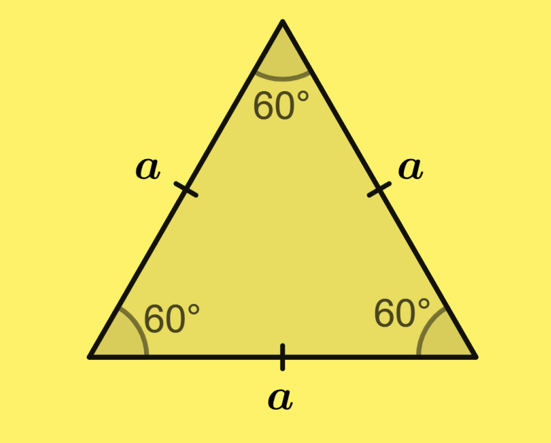
Triângulo Equilátero
É o triângulo com os três lados congruentes. Consequentemente, os três ângulos internos medem \(60^\circ\) cada. Em um equilátero, medianas, alturas, mediatrizes e bissetrizes coincidem; baricentro, incentro, circuncentro e ortocentro são o mesmo ponto.
Fórmulas essenciais (uma por linha)
As fórmulas vêm da decomposição do equilátero em dois triângulos retângulos \(30^\circ\!-\!60^\circ\!-\!90^\circ\) (lados \(1:\sqrt{3}:2\)).
Propriedades importantes
- Centros coincidentes: baricentro = incentro = circuncentro = ortocentro.
- Simetrias: três eixos de simetria; é um polígono regular de 3 lados.
- Relações com círculos: \(r=\frac{h}{3}\) e \(R=\frac{2h}{3}\).
Exemplos resolvidos
Exemplo 1 — lado dado \(\Rightarrow\) altura, área e perímetro
Considere um triângulo equilátero de lado \(a=10\ \text{cm}\). Calcule a altura, a área e o perímetro.
Ver solução
Exemplo 2 — perímetro conhecido \(\Rightarrow\) lado, altura e área
Um equilátero tem perímetro \(P=51\ \text{cm}\). Determine o lado, a altura e a área.
Ver solução
Exemplo 3 — inraio dado \(\Rightarrow\) lado, área e circunrádio
No triângulo equilátero, o inraio é \(r=3\ \text{cm}\). Encontre o lado, a área e o circunrádio.
Ver solução
Lista de exercícios — Triângulo Equilátero (múltipla escolha)
Use, se necessário: perímetro \(P=3a\), altura \(h=\frac{a\sqrt{3}}{2}\), área \(A=\frac{a^2\sqrt{3}}{4}\), inraio \(r=\frac{a\sqrt{3}}{6}\) e circunrádio \(R=\frac{a}{\sqrt{3}}\).
(1)
Um triângulo equilátero tem lado \(a=12\ \text{cm}\). Calcule o perímetro.
- 24 cm
- 30 cm
- 36 cm
- 48 cm
- 60 cm
Mostrar solução
(2)
Para \(a=8\ \text{cm}\), calcule a área.
- \(8\sqrt{3}\ \text{cm}^2\)
- \(12\sqrt{3}\ \text{cm}^2\)
- \(16\sqrt{3}\ \text{cm}^2\)
- \(24\sqrt{3}\ \text{cm}^2\)
- \(32\sqrt{3}\ \text{cm}^2\)
Mostrar solução
(3)
Se a área é \(27\sqrt{3}\ \text{cm}^2\), determine o lado do triângulo.
- \(6\ \text{cm}\)
- \(9\ \text{cm}\)
- \(6\sqrt{2}\ \text{cm}\)
- \(6\sqrt{3}\ \text{cm}\)
- \(9\sqrt{3}\ \text{cm}\)
Mostrar solução
(4)
A altura mede \(9\ \text{cm}\). Encontre o lado.
- \(9\ \text{cm}\)
- \(6\sqrt{3}\ \text{cm}\)
- \(12\ \text{cm}\)
- \(18\ \text{cm}\)
- \(3\sqrt{3}\ \text{cm}\)
Mostrar solução
(5)
O inraio é \(4\ \text{cm}\). Calcule o perímetro do triângulo.
- \(12\sqrt{3}\ \text{cm}\)
- \(18\sqrt{3}\ \text{cm}\)
- \(24\sqrt{3}\ \text{cm}\)
- \(36\ \text{cm}\)
- \(48\ \text{cm}\)
Mostrar solução
(6)
O circunrádio é \(5\ \text{cm}\). Calcule a área.
- \(25\sqrt{3}/2\)
- \(75\sqrt{3}/4\)
- \(50\sqrt{3}/3\)
- \(25\sqrt{3}/3\)
- \(15\sqrt{3}\)
Mostrar solução
(7)
Com lado \(a=10\ \text{cm}\), determine a altura.
- \(4\sqrt{3}\ \text{cm}\)
- \(5\sqrt{3}\ \text{cm}\)
- \(10\sqrt{3}/4\ \text{cm}\)
- \(10\sqrt{2}/2\ \text{cm}\)
- \(3\sqrt{3}\ \text{cm}\)
Mostrar solução
(8)
Uma peça é formada por \(20\) triângulos equiláteros de lado \(15\ \text{cm}\). Calcule a área total.
- \(375\sqrt{3}\ \text{cm}^2\)
- \(750\sqrt{3}\ \text{cm}^2\)
- \(1125\sqrt{3}\ \text{cm}^2\)
- \(1500\sqrt{3}\ \text{cm}^2\)
- \(2250\sqrt{3}\ \text{cm}^2\)
Mostrar solução
(9)
Um triângulo equilátero está inscrito em uma circunferência de raio \(9\ \text{cm}\). Calcule o perímetro do triângulo.
- \(18\sqrt{3}\ \text{cm}\)
- \(24\sqrt{3}\ \text{cm}\)
- \(27\sqrt{3}\ \text{cm}\)
- \(30\sqrt{3}\ \text{cm}\)
- \(36\sqrt{3}\ \text{cm}\)
Mostrar solução
(10)
Um triângulo equilátero circunscreve uma circunferência de raio \(6\ \text{cm}\). Calcule a área do triângulo.
- \(72\sqrt{3}\ \text{cm}^2\)
- \(96\sqrt{3}\ \text{cm}^2\)
- \(108\sqrt{3}\ \text{cm}^2\)
- \(120\sqrt{3}\ \text{cm}^2\)
- \(144\sqrt{3}\ \text{cm}^2\)
Mostrar solução
Resumo rápido
Veja também: Área de Triângulo, Área de Polígonos Regulares, Lei dos Senos, Lei do Cosseno.