Na figura abaixo estão representados os gráficos de uma parábola e de uma reta. O ponto \( P = (a,b) \) é um dos pontos de interseção da reta com a parábola.
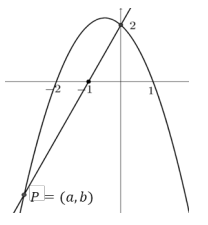
O valor de \( a + b \) é:
-
a) \(-7,5\)
b) \(-7\)
c) \(-6,5\)
d) \(-6\)
I) Determinando a equação da reta:
A reta passa pelos pontos \( (-1,0) \) e \( (0,2) \). Sua inclinação é: \[ m = \frac{2-0}{0-(-1)} = \frac{2}{1} = 2 \] Logo, a equação é: \[ y = 2x + 2 \]
II) Determinando a equação da parábola:
Pela figura, a parábola tem raízes em \( x=-2 \) e \( x=1 \). Podemos escrever: \[ y = p(x+2)(x-1) \] Como o ponto \( (0,2) \) pertence à parábola: \[ 2 = p \cdot 2 \cdot (-1) \Rightarrow p=-1 \] Assim, a parábola é: \[ y = -x^2 – x + 2 \]
III) Encontrando o ponto de interseção P(a,b):
Igualando as equações: \[ 2x+2 = -x^2-x+2 \] \[ x^2+3x=0 \Rightarrow x(x+3)=0 \Rightarrow x=0 \text{ ou } x=-3 \] Ponto \( P(a,b) = (-3,-4) \), pois é o ponto à esquerda.
IV) Soma dos valores:
\[ a+b = -3 + (-4) = -7 \]
Resposta Final: Alternativa B.
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo: