Esfera
A esfera é o conjunto dos pontos do espaço que estão a uma mesma distância \(r\) (raio) de um ponto fixo chamado centro. É um dos principais corpos redondos, ao lado do cilindro e do cone.
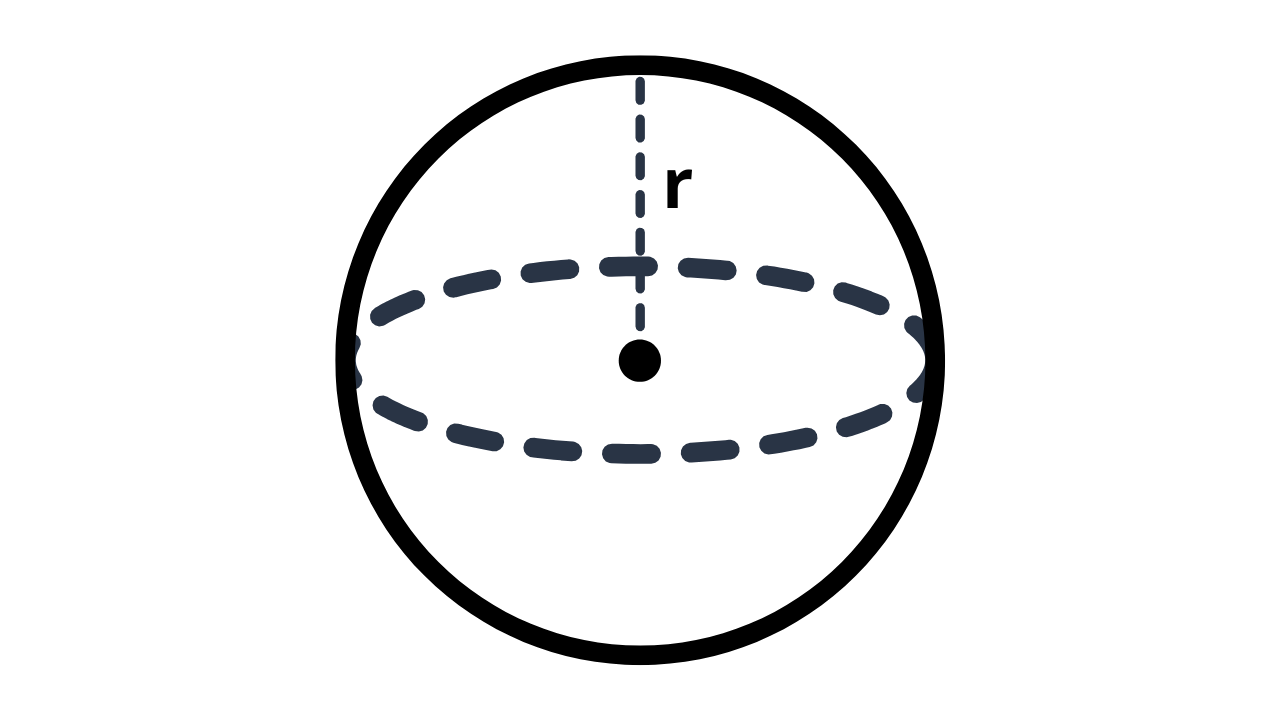
Notação: \(r\) = raio, \(d=2r\) = diâmetro, \(A\) = área da superfície, \(V\) = volume. Use \(\pi\approx3{,}1416\).
Elementos e ideias-chave
- Centro e raio \(r\); o diâmetro é \(d=2r\).
- Círculo máximo (ou grande círculo): seção de maior área, de raio \(r\).
- Casca esférica: superfície da esfera. O sólido preenchido também costuma ser chamado de esfera no ensino básico.
Área: \(\displaystyle A=4\pi r^2\).
Volume: \(\displaystyle V=\frac{4}{3}\pi r^3\).
Escala: se \(r\to k r\), então \(A\to k^2A\) e \(V\to k^3V\).
Relação de Arquimedes com o cilindro
Para uma esfera de raio \(r\) inscrita em um cilíndro de raio \(r\) e altura \(2r\):
- Volume da esfera é \(2/3\) do volume do cilindro: \(\displaystyle \frac{V_{\text{esf}}}{V_{\text{cil}}}=\frac{\frac{4}{3}\pi r^3}{2\pi r^3}=\frac{2}{3}\).
- Área da esfera é igual à área lateral do cilindro: \(4\pi r^2=2\pi r \cdot 2r\).
Esse resultado foi descoberto por Arquimedes e é um dos mais belos fatos da Geometria.
Partes da esfera: calota, zona e setor
- Calota esférica (tampa): porção limitada por um plano a altura \(h\) do topo. Para uma esfera de raio \(R\):
Área da calota: \(\displaystyle A=2\pi R h\).
Volume da calota: \(\displaystyle V=\frac{\pi h^2(3R-h)}{3}\). - Zona esférica (faixa entre dois planos paralelos): área depende apenas da altura \(h\): \(\displaystyle A=2\pi R h\).
- Setor esférico (tipo “fatia” com zona de altura \(h\)): volume \(\displaystyle V=\frac{2\pi R^2 h}{3}\).
Esfera inscrita/circunscrita em sólidos
| Cenário | Raio | Observação |
|---|---|---|
| Esfera inscrita num cubo (hexaedro) de aresta \(a\) | \(r=\dfrac{a}{2}\) | Toca o centro de cada face. |
| Esfera circunscrita ao cubo (passa pelos vértices) | \(R=\dfrac{\sqrt3}{2}\,a\) | Metade da diagonal espacial do cubo. |
| Esfera inscrita em cilindro \(r, h=2r\) | \(r\) (o mesmo do cilindro) | Relação \(V_{\text{esf}}/V_{\text{cil}}=2/3\). |
Equação da esfera (Geometria Analítica)
Com centro \(C(x_0,y_0,z_0)\) e raio \(r\):
Na forma geral \(x^2+y^2+z^2+Ax+By+Cz+D=0\), obtenha o centro completando quadrados: \(x^2+Ax=(x+\tfrac{A}{2})^2-\tfrac{A^2}{4}\) etc., e depois compare com \(r^2\).
Exemplos resolvidos
1) Pintura de uma bola
Uma bola tem raio \(11\) cm. Quantos cm² de tinta são necessários para cobrir a superfície?
Ver solução
Área \(A=4\pi r^2=4\pi\cdot121=484\pi\approx 1\,520{,}5\ \text{cm}^2\).
2) Esfera em cilindro
Um cilindro de raio \(r\) e altura \(2r\) contém uma esfera justaposta. Que fração do volume do cilindro é ocupada pela esfera?
Ver solução
\(V_{\text{esf}}=\frac{4}{3}\pi r^3\) e \(V_{\text{cil}}=\pi r^2\cdot2r=2\pi r^3\). Razão \(=\frac{4/3}{2}=\mathbf{2/3}\).
3) Calota esférica
Numa esfera de raio \(R=12\) cm recorta-se uma calota de altura \(h=3\) cm. Calcule área e volume da calota.
Ver solução
Área \(=2\pi R h=72\pi\ \text{cm}^2\). Volume \(=\dfrac{\pi h^2(3R-h)}{3}=99\pi\ \text{cm}^3\).
4) Equação da esfera a partir de dois pontos
Encontre a equação da esfera com centro em \(C(2,-1,3)\) que passa por \(P(6,1,0)\).
Ver solução
Raio: \(r=|CP|=\sqrt{(6-2)^2+(1+1)^2+(0-3)^2}=\sqrt{16+4+9}=\sqrt{29}\). Equação: \((x-2)^2+(y+1)^2+(z-3)^2=29\).
Exercícios propostos (com gabarito em abre/fecha)
1) Área e custo
Uma esfera de raio \(9\) cm será pintada a R$ \(0{,}04\)/cm². Qual o custo?
- R$ 40,60
- R$ 36,00
- R$ 32,60
- R$ 28,00
Gabarito
\(A=4\pi r^2=324\pi\approx 1\,017{,}9\). Custo ≈ R$ \(40{,}72\) → melhor aproximação: A.
2) Volume de uma bola
Uma bola tem diâmetro \(20\) cm. O volume é aproximadamente:
- 3 350 cm³
- 4 190 cm³
- 4 190 π cm³
- —
Gabarito
\(r=10\). \(V=\frac{4}{3}\pi 10^3\approx 4\,188{,}79\) → B.
3) Esfera inscrita no cubo
Num cubo de aresta \(a\), qual o raio da esfera inscrita e sua área?
- \(r=a\); \(A=4\pi a^2\)
- \(r=a/2\); \(A=\pi a^2\)
- \(r=a/2\); \(A=4\pi a^2\)
- \(r=a/\sqrt2\); \(A=2\pi a^2\)
Gabarito
\(r=a/2\). Área \(=4\pi (a/2)^2=\pi a^2\) → alternativa B.
4) Zona esférica
Numa esfera de raio \(R=10\) cm, uma faixa (zona) de altura \(h=4\) cm tem área:
- \(8\pi\)
- \(20\pi\)
- \(40\pi\)
- \(80\pi\)
Gabarito
\(A=2\pi R h=2\pi\cdot10\cdot4=80\pi\) → D.
5) Setor esférico
Para uma esfera de raio \(R\), um setor com zona de altura \(h\) tem volume:
- \(\dfrac{2\pi R^2 h}{3}\)
- \(\dfrac{\pi h^2(3R-h)}{3}\)
- \(2\pi Rh\)
- \(\dfrac{4}{3}\pi R^3\)
Gabarito
A. (As demais são: calota, área da zona, volume da esfera.)
6) Empacotamento
Qual a razão \(V_{\text{esfera}}/V_{\text{cilindro}}\) para uma esfera inscrita em cilindro de mesmo raio e altura \(2r\)?
- 1/2
- 2/3
- 3/4
- 4/5
Gabarito
\(\frac{2}{3}\) → B.
7) Centro e raio a partir da forma geral
Encontre centro e raio de \(x^2+y^2+z^2-4x+6y-2z-11=0\).
- \(C(2,-3,1)\), \(r=3\)
- \(C(2,-3,1)\), \(r=4\)
- \(C(-2,3,-1)\), \(r=4\)
- \(C(2,-3,1)\), \(r=5\)
Gabarito
Completando quadrados: \((x-2)^2+(y+3)^2+(z-1)^2=25\) → centro \(C(2,-3,1)\), raio \(r=5\). Alternativa D.
8) Calota em porcentagem do volume
Numa esfera de raio \(R\), uma calota de altura \(h=R\) ocupa qual fração do volume?
- 1/2
- 5/8
- 2/3
- 3/4
Gabarito
\(V=\frac{\pi h^2(3R-h)}{3}=\frac{2}{3}\pi R^3\). Fração \(=\frac{1}{2}\) → A.
9) Esfera circunscrita ao cubo
Para cubo de aresta \(a\), o raio da esfera que passa pelos vértices é:
- \(a/2\)
- \(\sqrt2\,a/2\)
- \(\sqrt3\,a/2\)
- \(\sqrt3\,a\)
Gabarito
Metade da diagonal espacial: \(R=\frac{\sqrt3}{2}a\) → C.
10) Mistura de esferas
Fundem-se 8 bolinhas idênticas de raio \(2\) cm para formar uma única esfera. Qual o raio da nova esfera?
- 4 cm
- 6 cm
- \(2\sqrt[3]{8}\) cm
- \(4\sqrt[3]{2}\) cm
Gabarito
Conserva volume: \(8\cdot \frac{4}{3}\pi 2^3=\frac{4}{3}\pi R^3\Rightarrow R^3=64\Rightarrow R=4\) cm → A.
Continue estudando
- Resumo geral de Corpos redondos — Cilindro • Cone.
- Sólidos de Platão — compare com poliedros regulares.
- Hexaedro (cubo) • Octaedro • Icosaedro