Função e Conjuntos

Este guia conecta os conceitos de conjuntos e funções, tema recorrente no ENEM e em concursos. Recomendamos usar junto os materiais do Mapa Mental de Funções e o Banco de Questões para treinar.

Função x Conjuntos: diagrama, pares e tabela

Definição formal: \( f: A \to B \) é função se, para todo \(x \in A\), existe um único \(y \in B\) tal que \(y=f(x)\).

Vocabulário essencial

Domínio (\(A\)): de onde saem os valores de entrada.
Contradomínio (\(B\)): conjunto-alvo dos resultados possíveis.
Imagem (\(\mathrm{Im}(f)\)): subconjunto de \(B\) formado pelos valores efetivamente obtidos.
Representações: pares ordenados, tabela, lei de formação e diagrama de setas.

Leituras relacionadas (internas)

Conjuntos Numéricos Operações com Frações Equações do 1º Grau Função do 2º Grau Logaritmos

📘 Reforço para estudos: eBook Fórmulas Matemática — todas as fórmulas de funções, conjuntos, álgebra e mais em um único PDF para consulta rápida.

Exemplos comentados

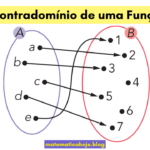
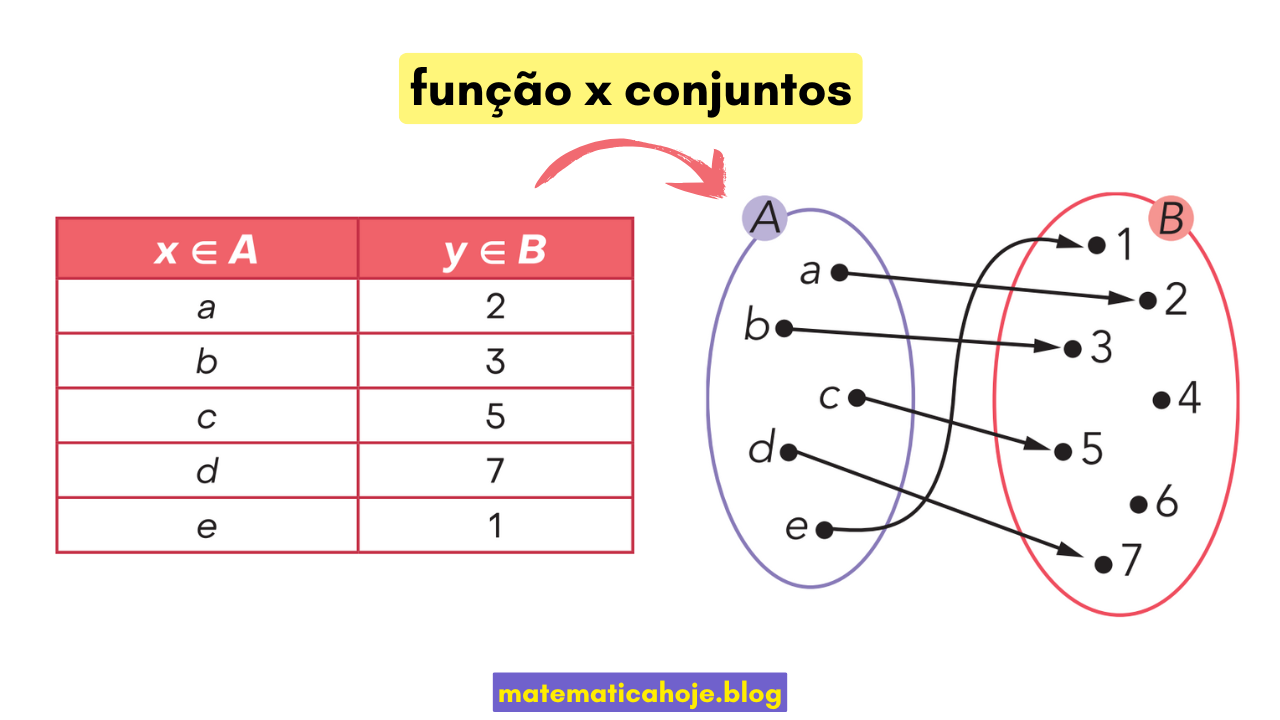
Exemplo 1 — Diagrama de setas

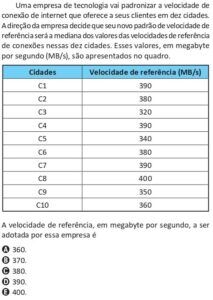
Considere \(A=\{a,b,c,d,e\}\) e \(B=\{1,2,3,4,5,6,7\}\) como na figura. As associações são: \(a\mapsto2\), \(b\mapsto3\), \(c\mapsto5\), \(d\mapsto7\), \(e\mapsto1\).

Domínio: \(A\)
Contradomínio: \(B\)
Imagem: \(\{1,2,3,5,7\}\)

Exemplo 2 — Tabela e pares ordenados

\(x\in A\)	\(y\in B\)
a	2
b	3
c	5
d	7
e	1

Como pares ordenados: \(\{(a,2),(b,3),(c,5),(d,7),(e,1)\}\). Cada elemento de \(A\) aparece uma única vez na 1ª coordenada ⇒ é função.

Exemplo 3 — Lei de formação numérica

Seja \(A=\{0,1,2,3\}\) e \(f:A\to \mathbb{N}\) tal que \(f(x)=2x+1\).

\(f(0)=2\cdot0+1=1\)
\(f(1)=2\cdot1+1=3\)
\(f(2)=2\cdot2+1=5\)
\(f(3)=2\cdot3+1=7\)

Imagem: \(\{1,3,5,7\}\). Veja também funções polinomiais e seu crescimento.

🎁 Baixe os 10 eBooks de Matemática (coleção completa)

Exercícios com gabarito (passo a passo)

Dica: Para revisar notação de conjuntos e subconjuntos, consulte o artigo Conjuntos Numéricos.

1) Seja \(R=\{(a,1),(a,2),(b,3)\}\) com domínio \(A=\{a,b\}\) e contradomínio \(B=\{1,2,3\}\). \(R\) é função de \(A\) em \(B\)?

Sim, pois cada elemento de \(A\) tem imagem.
Não, pois \(a\) possui duas imagens.
Sim, pois \(B\) tem três elementos.
Não, pois \(b\) não tem imagem.

Ver solução

Em função, cada \(x\in A\) deve ter uma única imagem. Em \(R\), aparecem \((a,1)\) e \((a,2)\) ⇒ duas imagens para \(a\). Logo, não é função.

2) Considere \(f:A\to B\) dada pela tabela do diagrama (a→2, b→3, c→5, d→7, e→1). Determine \(\mathrm{Im}(f)\).

\(\{2,3,4,5\}\)
\(\{1,2,3,5,7\}\)
\(\{1,2,3,4,5,6,7\}\)
\(\{a,b,c,d,e\}\)

Ver solução

Valores obtidos: 2,3,5,7,1
Ordenando: \(\{1,2,3,5,7\}\).

3) Seja \(A=\{0,1,2,3\}\) e \(f(x)=2x+1\). Calcule \(f(A)\).

\(\{1,2,3,4\}\)
\(\{1,3,5,7\}\)
\(\{0,2,4,6\}\)
\(\{3,5,7,9\}\)

Ver solução

\(f(0)=1\)
\(f(1)=3\)
\(f(2)=5\)
\(f(3)=7\)
Portanto, \(f(A)=\{1,3,5,7\}\).

4) Em \(A=\{-2,-1,0,1,2\}\), considere \(g(x)=x^2\). Qual é a imagem?

\(\{-4,-1,0,1,4\}\)
\(\{0,1,4\}\)
\(\{-2,-1,0,1,2\}\)
\(\{1,2,3,4,5\}\)

Ver solução

\(g(-2)=4\)
\(g(-1)=1\)
\(g(0)=0\)
\(g(1)=1\)
\(g(2)=4\)
Distintos ⇒ \(\{0,1,4\}\).

5) A relação \(h=\{(a,2),(b,2),(c,2)\}\) com \(A=\{a,b,c\}\) e \(B=\{1,2,3\}\) é função? Classifique quanto à sobrejetividade.

Não é função.
É função e é sobrejetora.
É função e não é sobrejetora.
É função e é injetora.

Ver solução

É função: cada elemento de \(A\) tem uma imagem (todas iguais a 2).
Não é sobrejetora: elementos 1 e 3 de \(B\) não são atingidos.
Também não é injetora, pois várias entradas têm a mesma imagem.

6) Seja \(A=\{1,2,3,4\}\) e \(p(x)=\begin{cases}x/2,&x \text{ par}\\ 3x+1,&x \text{ ímpar}\end{cases}\). Calcule \(p(A)\).

\(\{1,2,3,4\}\)
\(\{2,4,6,8\}\)
\(\{2,4,10,1.5\}\)
\(\{2,7,10,2\}\)

Ver solução

Para ímpar: \(3x+1\). Para par: \(x/2\).
\(x=1\) (ímpar) ⇒ \(3(1)+1=4\)
\(x=2\) (par) ⇒ \(2/2=1\)
\(x=3\) (ímpar) ⇒ \(3(3)+1=10\)
\(x=4\) (par) ⇒ \(4/2=2\)
Logo, \(p(A)=\{4,1,10,2\}\) = \(\{1,2,4,10\}\).